Use the Substitution Formula in Theorem 7 to evaluate the integral.a.

b.

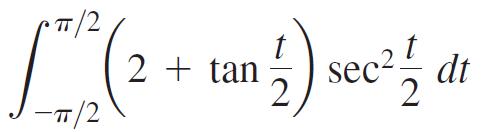
THEOREM 7-Substitution in Definite Integrals If g' is continuous on the interval [a, b] and f is continuous on the range of g(x) = u, then rg(b) [ f(g(x)) g'(x) dx = - f(u) du. g(a) Proof Let F denote any antiderivative of f. Then, [ f(g(x a f(g(x)) g'(x) dx = F(g(x)) = F(u) |x=b = F(g(b)) - F(g(a)) u=g(b) Ju=g(a) g(b) - s = g(a) x=a f(u) du. dx = F(g(x)) F'(g(x))g'(x) f(g(x))g'(x) Fundamental Theorem, Part 2 To use the formula, make the same u-substitution u = g(x) and du = g'(x) dx you would use to evaluate the corresponding indefinite integral. Then integrate the transformed integral with respect to u from the value g(a) (the value of u at x = a) to the value g(b) (the value of u at x = b).