When a circle rolls on the inside of a fixed circle, any point P on the circumference of the rolling circle describes a hypocycloid. Let the fixed circle be x² + y² = a², let the radius of the rolling circle be b, and let the initial position of the tracing point P be A(a, 0). Find parametric equations for the hypocycloid, using as the parameter the angle θ from the positive x-axis to the line joining the circles’ centers. In particular, if b = a/4, as in the accompanying figure, show that the hypocycloid is the astroid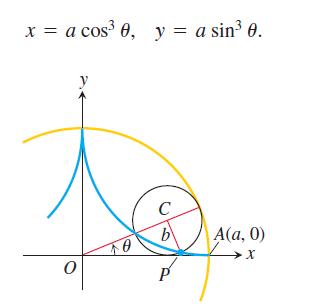

x = a cos 0, y = a sin 0. O 10 C b P A(a,0) LX