You may recall that the point inside a triangle that lies one-third of the way from each side toward the opposite vertex is the point where the triangle’s three medians intersect. Show that the centroid lies at the intersection of the medians by showing that it too lies one-third of the way from each side toward the opposite vertex. To do so, take the following steps.

i) Stand one side of the triangle on the x-axis as in part (b) of the accompanying figure. Express dm in terms of L and dy.

ii) Use similar triangles to show that L = (b/h)(h - y). Substitute this expression for L in your formula for dm.

iii) Show that ȳ = h/3.

iv) Extend the argument to the other sides.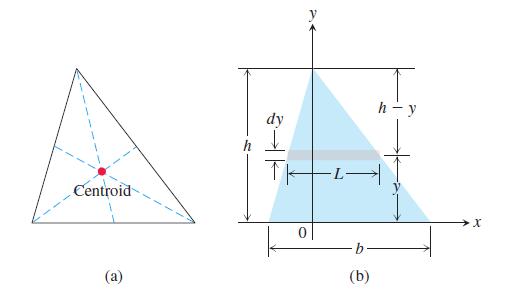

Centroid (a) 0 -L| b (b) y x