Question: (a) If x(t) has the Fourier and y(t) = x(t - t 0 ), show that Y n = X n e -j2Ïnf0t0 where the

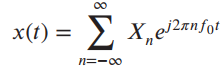
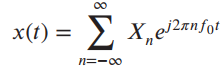
(a) If x(t) has the Fourier ο0 j2πnfo 1 χ() ΣX,emfof x(t)

and y(t) = x(t - t0), show that Yn = Xne-j2Ï€nf0t0 where the Yn's are the Fourier coefficient for y(t).

(b) Verify the theorem proved in part (a) by examining the Fourier coefficients for x(t) = cos(ω0t) and y(t) = sin(ω0t).

0 j2nfo 1 () X,emfof x(t)

Step by Step Solution

★★★★★

3.58 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a The integral for Y n is Let t t t 0 which results in b Note tha... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Principles Communications Systems Questions!

Q:

The Willowbrook School staff has accepted your systems design and your design specifications. Your group recommended installing a server and three personal computers as clients on a local area...

Q:

Consider the system in figure. The input signal x c (t) has the Fourier transform shown in figure with ? 0 = 2? (1000) radians/second. The discrete-time system is an ideal lowpass filter with...

Q:

A complex-valued continuous-time signal x c (t) has the Fourier transform shown in figure, where (? 2 ? ? 1 ) = ??. This signal is sampled to produce the sequence x[n] = x c (nT). (a) Sketch the...

Q:

This problem explores the effect of interchanging the order of two operations on a signal, namely, sampling and performing a memoryless nonlinear operation. (a) Consider the two signal-processing...

Q:

MATH 251 Spring 2014 Final Exam Simon Fraser University 23 April 2014, 7:00-10:00pm Instructor: Weiran Sun Last Name: First Name: SFU ID: @sfu.ca Signature: Instructions Question Maximum 1. Please do...

Q:

9. (a) Let X be an exponential random variable. Show that P(X > s+t|X > s) =P(X > t) for all s, t > 0. (b) Let X be a random variable having support [0, co) and a cdf F differentiable on (0, co)....

Q:

Maddala (1992, pp. 120-127). Consider the simple linear regression yi = + Xi + ui i = 1, 2, . . ., n. where and are scalars and ui IIN(0, 2). For Ho; = 0, (a) Derive the Likelihood Ratio (LR)...

Q:

The amount of time, in minutes, that a person must wait for a bus is uniformly distributed between 0 and 15 minutes, inclusive. What is the probability that a person waits fewer than 12.5 minutes?...

Q:

Please tell me how to make this code below work on onlinegdb.com, I can not get this c code to show the 0 s and 1 s , the only output i get is usage.a . out speed.Please show screenshots of how to...

Q:

Let S be a nonempty subset of a linear space and let m dim cone S. For every x cone S, there exist x1,x2,...,xn S and α1, α2, . . ., αn + Such that x =...

Q:

Let X represent the amount of time students use when they take a final exam. The allotted time is up to 2 hours. Suppose X is continuous and its pdf is below. f(x) = (3/8)x 2 where 0

Q:

For the pin-connected truss shown below use the virtual work method to determine the vertical displacement of joint A if members AE and ED experience a temperature increase of ?T = 250?C. Assume both...

Q:

The spending variance can be separated into two components. Name and briefly describe them.

Q:

Find a set of parametric equations of the line with the given characteristics. ( Use t for the parameter. Enter your answers as a The line passes through the point ( - 3 , 5 , 6 ) and is...

Q:

A high-speed flywheel in a motor is spinning at 500 rpm when a power failure suddenly occurs. The flywheel has mass 40.0 kg and diameter 75.0 cm. The power is off for 30.0 s, and during this time the...

Q:

An encryption-decryption system consists of three elements: encode, transmit, and decode. A faulty encode occurs in 0.5% of the messages processed, transmission errors occur in 1% of the messages,...

Q:

Should managers actively seek substitutes for leadership? Why or why not?

Q:

Are there some jobs for which there are no substitutes? Provide examples.

Q:

Based on each positions power base(s), what outcomes would a person in this position be likely to experience if they were acting as a leader?

Q:

=+.** Suppose that your tastes were instead characterized by the function u1x1 ,x2 2 5 10.5x1 2r 1 0.5x2 2r 2 21/r

Q:

A rectangular conducting plate lies in the xy plane, occupying the region 0

Q:

Two conducting plates, each 3 6 cm, and three slabs of dielectric, each 1 3 6 cm, and having dielectric constants of 1, 2, and 3, are assembled into a capacitor with d = 3 cm. Determine the two...

Q:

Show that in a homogeneous medium of conductivity , the potential field V satisfies Laplaces equation if any volume charge density present does not vary with time.

Q:

Suppose you got your first job with the DC Police Department as a data analysts.Your first assignment was to analysis a dataset on 81 drunk drivers who were arrested in the preceding month in...

Q:

(Estimated time allowance: 5 minutes) Use the data from the financial statements of a company shown here (or in excel) to answer the question below (bottom of last financial statement). To get the...

Q:

ADJUSTMENTS: for the month of August. a. the business rents an office at a monthly rate of $1,600; on August 1, four months rent was paid in advance. b. Office supplies on hand at August 31 amounted...