(Chi-squared pdf) Consider the random variable Y = N i = 1 where the X i s are independent Gaussian random variables with pdfs n(0,Ï).

(Chi-squared pdf) Consider the random variable Y = ˆ‘^N _{i = 1} where the X_i€™s are independent Gaussian random variables with pdfs n(0,σ).

(a) Show that the characteristic function of X²_i is M_X²_i (jv) = (1 - 2jvσ²)^-1/2

(b) Show that the pdf of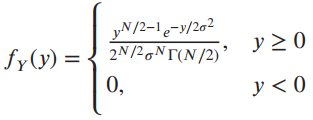  

where F(x) is the gamma function, which, for x = n, an integer is F(n) = (n - 1)!. This pdf is known as the x² (chi-squared) pdf with N degrees of freedom. Use the Fourier-transform pair 

(c) Show that for N large, the x² pdf can be approximated as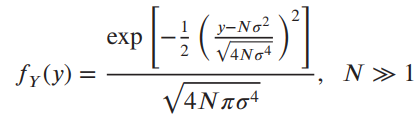 

Use the central-limit theorem. Since the x_i €™s are independent,

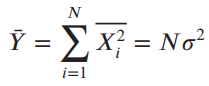
and

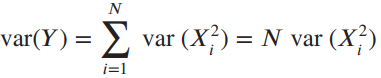
(d) Compare the approximation obtained in part (c) with f_Y (y) for N = 2, 4, 8.

(e) Let R² = Y. Show that the pdf of R for N = 2 is Rayleigh.

yN /2=1 e=y/202 fy(y) = { 2N/2oN[(N/2)' 0, y < 0 y/-1e-y/ /2 (N/2) /21 +(1-j)-/2|