Consider the hypotheses

H₁ : Z = N and H₂ : Z = S + N

where S and N are independent random variables with the pdfs

f_s(x) = 2e^-2x u(x) and f_N(x) = 10e^-10x u(x)

(a) Show that

f_z(z|H₂) = 10e^-10x(x)

and

f_z(z|H₂) = 2.5 (e^-2x - e^-10z) u(x)

(b) Find the likelihood ratio Λ(Z).

(c) If P(H₁) = 1/3, P(H₂) = 2/3, c₁₂ = c₂₁ =7, and c₁₁ = c₂₂ = 0, find the threshold for a Bayes test.

(d) Show that the likelihood ratio test for part (c) can be reduced to

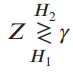Find the numerical value of y for the Bayes test of part (c).

(e) Find the risk for the Bayes test of part (c).

(f) Find the threshold for a Neyman-Pearson test with P_F less than or equal to 10^-3. Find P_D for this threshold.

(g) Reducing the Neyman-Pearson test of part (f) to the form

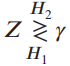
find P_F and P_D for arbitrary y. Plot the ROC.

Z ZY H1 Z ZY , H1