Question: Let the sample functions of a random process be given by X(t) = A cos 2Ïf 0 t where Ï 0 is fixed and A

Let the sample functions of a random process be given by

X(t) = A cos 2Ï€f0t

where ω0 is fixed and A has the pdf 

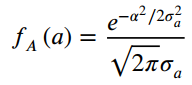
e-a? /20, fA (a) = V2πσ, τσ α

This random process is passed through an ideal integrator to give a random process Y(t).

(a) Find an expression for the sample functions of the output process Y(t).

(b) Write down an expression for the pdf of Y(t) at time t0. Note that sin 2Ï€f0t0 is jsut a constant. 

(c) Is Y(t) stationary? Is it ergodic?

e-a? /20, fA (a) = V2,

Step by Step Solution

★★★★★

3.47 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a The sample functions at the integrator output are ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Principles Communications Systems Questions!

Q:

Consider the random process of Problem 7.4. (a) Find the time-average mean and the auto correlation function. (b) Find the ensemble-average mean and the auto correlation function. (c) Is this process...

Q:

Given two independent, wide-sense stationary random processes X(t) and Y(t) with auto correlation functions R x () and R Y (), respectively. (a) Show that the auto correlation function R Z () of...

Q:

A random process is composed of sample functions of the form where n(t) is a wide-sense stationary random process with the auto correlation function R n (Ï), and n k = n(kT s ). (a) If T s is...

Q:

Problem 1. Problem 2. Problem 3. Problem 4. 1. (10 points) Let X; for i =1,2,..., n be independent and identically distributed random variables with mean u > 0 and standard deviation o > 0. When we...

Q:

Module 2Demand Theory and Estimation Activity 4Case 3 Using SPSS, MS Excel or other statistical software package, run the given data and answer the following in MS Word. Assume that Electronix, Inc.,...

Q:

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

Q:

Given: . Probability Density Function (PDF): 0(1 -2)0-1 if0 0 is an unknown parameter. Based on these observations, determine an estimate of & using (a) maximum likelihood (b) method of moments 2....

Q:

Given: . Probability Density Function (PDF): 0(1 -2)0-1 if0 0 is an unknown parameter. Based on these observations, determine an estimate of & using (a) maximum likelihood (b) method of moments 2....

Q:

Given: . Probability Density Function (PDF): 0(1 -2)0-1 if0 0 is an unknown parameter. Based on these observations, determine an estimate of & using (a) maximum likelihood (b) method of moments 2....

Q:

Given: . Probability Density Function (PDF): 0(1 -2)0-1 if0 0 is an unknown parameter. Based on these observations, determine an estimate of & using (a) maximum likelihood (b) method of moments 2....

Q:

An object with a height of 3.4 cm is 28 cm from a (thin) convex lens. The image is 56 cm from the lens on the same side as the object. What is the focal length? Select the correct answer from the...

Q:

Identify the problems (3) as set out in the case study and discuss actions the company can take to solve the problem identified above. The subprime mortgage crisis of 2008 and the now famous failure...

Q:

Data type selection is usually dictated by the nature of the data and by the intended use. True False

Q:

12. How is goodwill tested for impairment?

Q:

Three point charges are positioned in the x-y plane as follows: 5 nC at y = 5 cm, 10 nC at y = 5 cm, and 15 nC at x = 5 cm. Find the required x-y coordinates of a 20-nC fourth charge that will...

Q:

Point charges of 1 nC and 2 nC are located at (0, 0, 0) and (1, 1, 1), respectively, in free space. Determine the vector force acting on each charge.

Q:

Point charges of 50 nC each are located at A(1, 0, 0), B(1, 0, 0), C(0, 1, 0), and D(0,1, 0) in free space. Find the total force on the charge at A.

Q:

\ table [ [ , Returns ] , [ Year , x , Y , ] , [ 1 , 1 9 % , 1 5 % , ] , [ 2 , 2 2 , 3 4 , ] , [ 3 , 8 , 1 4 , ] , [ 4 , - 1 5 , - 2 0 , ] , [ 5 , 1 0 , 2 4 , ] ] Using the returns shown above,...

Q:

re Use the data for Starbucks (SBUX) and Google (GOOG) I to answer the following questions: a. What is the return for SBUX over the period without including its dividends? With the dividends? b. What...

Q:

The following two securities are currently trading in the economy. Suppose that annualized continuously compounded interest rate is r, and time to maturity is T. B = 0.90 0.4595 0.5172 2 0 Given...