Question: The a periodic auto correlation function of a binary code is of interest in some synchronization applications. In computing it, the code is not assumed

The a periodic auto correlation function of a binary code is of interest in some synchronization applications. In computing it, the code is not assumed to periodically repeat itself, but (10.130) is applied only to the overlapping part. For example, with the 3-chip Barker code of Table 9.12 the computation is as follows:

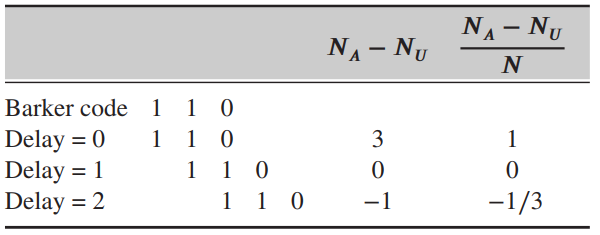NA- NU NA- NU 1 0 Barker code Delay = 0 Delay = 1 = 2 1 1 1 0 1 1 11 0 3 0 -1_ -1/3 For negative delays, we need not perform the calculation because auto correlation functions are even.
(a) Find the a periodic auto correlation functions of all the Barker sequences given in Table 9.12. What are the magnitudes of their maximum non-zero delay auto correlation values?

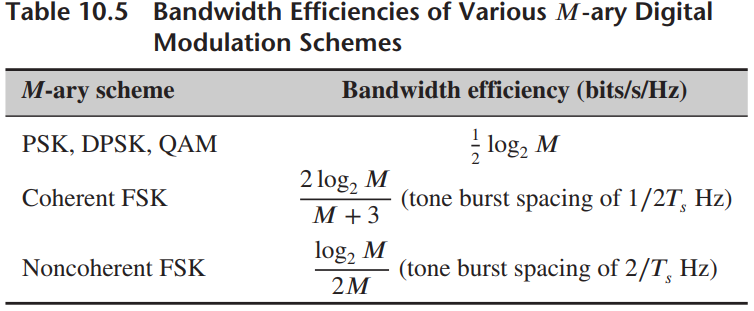
(b) Compute the a periodic auto correlation function of a 15-bit PN sequence. What is the magnitude of its maximum nonzero-delay auto correlation values? Note from Table 10.5 that this is not a Barker sequence.

Table 10.5 Bandwidth Efficiencies of Various M-ary Digital Modulation Schemes M-ary scheme Bandwidth efficiency (bits/s/

NA- NU NA- NU 1 0 Barker code Delay = 0 Delay

NA- NU NA- NU 1 0 Barker code Delay = 0 Delay = 1 = 2 1 1 1 0 1 1 11 0 3 0 -1_ -1/3 Table 10.5 Bandwidth Efficiencies of Various M-ary Digital Modulation Schemes M-ary scheme Bandwidth efficiency (bits/s/Hz) PSK, DPSK, QAM log, M 2 log, M Coherent FSK (tone burst spacing of 1/27, Hz) M +3 log, M Noncoherent FSK (tone burst spacing of 2/T, Hz) 2M

Step by Step Solution

★★★★★

3.53 Rating (174 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Lengths 11 and 13 are not included reference should be to Table 1012 b Th... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Principles Communications Systems Questions!

The a periodic auto correlation function for a real-valued stable sequence x[n] is defined as (a) Show that the z-transform of c x [n] is? C xx (z) = X(z) X(z?1). ?Determine the region of convergence...

The input to a low pass filter with impulse response h(t) = exp (-10t) u(t) is white, Gaussian noise with single-sided power spectral density of 2 W/Hz. Obtain the following: (a) The mean of the...

Obtain the auto correlation functions and power spectral densities of the outputs of the following systems with the input auto correlation functions or power spectral densities given. (a) Transfer...

DON'T SUMMARIZE JUST PARAGRAPH OF WHAT YOU THOUGHT/LEARNED CHAPTER 13 - The phrase "garbage in, garbage out" highlights the importance of input controls. If the data entered into a system are...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Python and most Python libraries are free to download or use, though many users use Python through a paid service. Paid services help IT organizations manage the risks associated with the use of...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

answer the following questions: What are your moral obligations as professionals to prevent such things from happening? What guidance do the professional codes provide (cite specific code sections in...

A creative engineer suggests structuring the TLB so that not all the bits of the presented address need match to result in a hit. Suggest how this might be achieved, and what might be the costs and...

Why are warranty liabilities usually recognized on the balance sheet as liabilities even when they are uncertain? Discuss.

A car accelerates uniformly from rest to a speed of 25 m/s over a distance of 200 meters. Calculate the acceleration of the car

Aher mary sunset viewings at SUNY Brochport, Anarda dueams of owning a waterfront home on Lake Ontarla. She finds her peritect houte lipted at $ 4 2 5 0 0 0 . L - ueraging the negptiation skils ohe...

4.1.10 A bus in a mass transit system is operating on a continuous route with intermediate stops. The arrival of the bus at a stop is classified into one of three states, namely 1. Early arrival; 2....

(a) The range of audible frequencies is from about 20 Hz to 20,000 Hz. What is the range of the wavelengths of audible sound in air? (b) The range of visible light extends from 400 nm to 700 nm. What...

A circular saw blade with radius 0.120 m starts from rest and turns in a vertical plane with a constant angular acceleration of 3.00 rev/s 2 . After the blade has turned through 155 rev, a small...

Conventional hot-water heaters consist of a tank of water maintained at a fixed temperature. The hot water is to be used when needed. The drawbacks are that energy is wasted because the tank loses...

The provided data is as follows; A-10, B-4, C-3, D-1, F-2. Question 22 that is referred to in the first question was found to be .1, or 10% Question 19 that is referred to in the second question was...

During 2021, Raines Umbrella Corporation had sales of $900,000. Cost of goods sold, administrative and selling expenses, and depreciation expenses were $575,000, $125,000, and $145,000, respectively....

Credit unions and Internet-only banks typically offer more attractive interest rates to both borrowers and savers. less attractive interest rates to both borrowers and savers. the same interest rates...