Question: Two Gaussian random variables X and Y, with zero means and variances Ï 2 , between which there is a correlation coefficient p, have a

Two Gaussian random variables X and Y, with zero means and variances Ïƒ², between which there is a correlation coefficient p, have a joint probability-density function given by

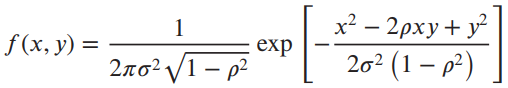
x² – 2pxy+ y f(x, y) = exp 2πσ2 V1 -ρ2 202 (1 – p²)

The marginal pdf of Y can be shown to be

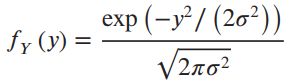
exp (-y²/ (2o²)) fy (y) = V2ло?

Find the conditional pdf f_X|Y(X | Y).

x 2pxy+ y f(x, y) = exp 22 V1 -2 202 (1 p) exp (-y/ (2o)) fy (y) = V2?

Step by Step Solution

★★★★★

3.44 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The conditional pdf f XY xy is given by Note that the conditional pdf of X given Y is Gaussian ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Principles Communications Systems Questions!

Two Gaussian random variables, X and Y, are in dependent. Their respective means are 5 and 3, and their respective variances are 1 and 2. (a) Write down expressions for their marginal pdfs. (b) Write...

Two Gaussian random variables, X and Y, are in dependent. Their respective means are 4 and 2, and their respective variances are 3 and 5. (a) Write down expressions for their marginal pdfs. (b) Write...

Two jointly Gaussian random variables, X and Y, have means of 1 and 2, and variances of 3 and 2, respectively. Their correlation coefficient is P xy = 0.2. A new random variable is defined as Z = 3X...

Allow X to signify the voltage at the yield of a mouthpiece, and assume that X has a uniform circulation on the stretch from ?1 to 1. The voltage is handled by a "hard limiter" with cutoff esteems...

Question: Talk about the accompanying inquiries completely The term Programming interface addresses ___? The clarification "event variable" is another name for... Case evaluation; For normal...

System update. Consider the following queueing system. Customers arrive in pairs according to a Poisson process with rate ? = 1 customer pair/minute. There is one server and room for two customers to...

Question: 1. In either Vanilla JavaScript or in the React framewok, a TODapplication that meets the following requirements: a. Show an unordered list of todo descriptions that starts as an empty...

Show all your workings kindly. Given that the probability of a student taking a statistics class is 0.83, and the probability of a student taking a calculus class and a statistics class is 0.66, what...

Discussion 5 Statistics 103 Winter quarter 2016 Topics covered EY = 0, sd(Y ) = 2 (5) = 0.1 1. Bivariate Normal. Assume the joint distribution of (X, Y ) is bivariate normal. Predict Y when the...

5. Consider a bivariate distribution with joint pdf given by f(x, y) = cexp 0, X and Y are bivariate Gaussian random variables with joint PDF exp ( (2 3) /4 (x-3)(y-1)/3+ (y-1)2/4 fx, x (x, y) = C 87...

A retailer receives a shipment of 12000 soybeans that will be used at a constant rate of 300 pounds per week. If the cost of storing the soybeans is 0.2 cents per pound per week, how much will the...

List three resistance to change strategies. Give an example when you would use each method or approach.

You are required to calculate for each product of the company as a whole: (a) Value of Stock at 31st December, 2016, at cost; (b) The amount of Gross Profit, as they would appear in the companys...

The CPI is a fixed-weighted measure. What does this mean? 16 Explain how the CPI is computed.

A particles velocity is described by the function v x = (t 2 - 7t + 10) m/s, where t is in s. a. At what times does the particle reach its turning points? b. What is the particles acceleration at...

A particles velocity is described by the function v x = k t 2 m/s, where k is a constant and t is in s. The particles position at t 0 = 0 s is x 0 = - 9.0 m. At t 1 = 3.0 s, the particle is at x 1 =...

A particles acceleration is described by the function a x = (10 t) m/s 2 , where t is in s. Its initial conditions are x 0 = 0 m and v 0x = 0 m/s at t = 0 s. a. At what time is the velocity again...

OMG Inc. has 5 million shares of common stock outstanding, 4 million shares of preferred stock outstanding, and 6,000 bonds. Suppose the common shares are selling for $27 per share, the preferred...

Suppose a company had an initial investment of $50,000. The cash flow for the next five years are $11,000, $15,000, $10,000, $10,000, and $12,000, respectively. What is the payback period? Number...

Investors require a 17% rate of return on Brooks Sisters' stock (rs = 17%). a.What would the value of Brooks's stock be if the previous dividend was D0 = $1.5 and if investors expect dividends to...