Question: Using x r (t) = m(t) cos(2Ïf c t) and e 0 (t) = 2 cos (2Ïf c t + θ) for the assumed Costas
Using xr(t) = m(t) cos(2πfct) and e0(t) = 2 cos (2πfct + θ) for the assumed Costas PLL input and VCO output, respectively, verify that all signals shown at the various points in Figure 4.26 are correct. Assuming that the VCO frequency deviation is defined by dθ / dt = -Kvev(t), where ev(t) is the VCO input and Kvis a positive constant, derive the phase plane. Using the phase plane, verify that the loop locks.
Figure 4.26
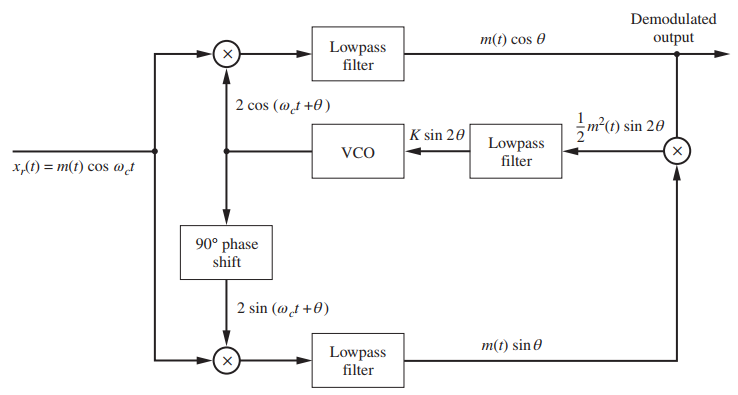
Demodulated m(t) cos 0 output Lowpass filter 2 cos (@t +0) m(1) sin 20 K sin 20 Lowpass filter VCO x,(1) = m(t) cos @d 90 phase shift 2 sin (@t +0) m(t) sin 0 Lowpass filter )
Step by Step Solution
3.31 Rating (148 Votes )
There are 3 Steps involved in it
The Costas PLL is shown in Figure 426 The output of the top multiplier is mtco... View full answer
Get step-by-step solutions from verified subject matter experts
Study Help