Question: 19. Let X be a nonnegative random variable with distribution function F. Define (a) Prove that R 0 I(t) dt = X. (b) By

19. Let X be a nonnegative random variable with distribution function F. Define

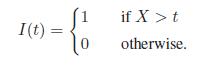
I(t)= if X > t otherwise.

(a) Prove that R ∞
0 I(t) dt = X.

(b) By calculating the expected value of both sides of part (a), prove that

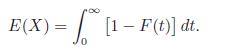
image text in transcribed

This is a special case of Theorem 6.2.

(c) For r > 0, use part

(b) to prove that

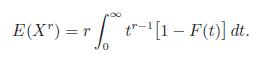
image text in transcribed

I(t)= if X > t otherwise.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

Q:

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Q:

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

Q:

17. Let X be a nonnegative random variable with distribution function F. Define I (t) = B 1 if X > t 0 otherwise. (a) Prove that # 0 I (t) dt = X. (b) By calculating the expected value of both sides...

Q:

16 Let X be a nonnegative random variable with distribution function F. Define 1(t)= = { b 1 if X > t 10 otherwise. (a) Prove that I(t)dt = X. (b) By calculating the expected value of both sides of...

Q:

i just need to solve part 1 please Part 1 Consider a network that has four nodes n1, n2, n3 and n4, and six directed arcs of the form a1 = (n1, n2), a2 = (n1, n3), a3 = (n2, n3 ), a4 = (n3), n2), a5...

Q:

1. Consider a network that has four nodes n1, n2, n3 and n4, and six directed arcs of the form a1 = (n1, n2), a2 = (n1, n3), a3 = (n2, n3 ), a4 = (n3), n2), a5 = (n2, n4) and a6 = (n3, n4), where the...

Q:

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

Q:

) Consider integer division of one two's-complement binary number by another. Programming languages may vary in the result when one argument is negative. What differing conventions might they be...

Q:

) Explain the collision detection mechanism applied in standard wired medium access control associated with CSMA and indicate why this might be unsuitable for wireless networks. [2 marks] (ii)...

Q:

applytuio a) SoC design involves dividing work between hardware and software as well as deciding the number of general-purpose and custom processors and co-processors to be used. What main factors...

Q:

Ullie Medical Supply is a retailer of home medical equipment. Last year, Ullies sales reve-nues totaled $ 6,800,000. Total expenses were $ 2,600,000. Of this amount, approximately $ 1,088,000 were...

Q:

Why is it useful to consider not only unconditional coverage but also conditional coverage?

Q:

Option premiums are set at predetermined levels by the exchange. True False

Q:

In the lab you place a beaker that is half full of water (density (w) on a scale. You now use a light string to suspend a piece of metal of volume V in the water. The metal is completely submerged,...