2.1. Let X X,, . . . be independent identically distributed positive random variables whose common distribution function is F. We interpret X X ... as successive bids on an asset offered for sale. Suppose that the policy is followed of accepting the first bid that exceeds some prescribed number A. Formally, the accepted bid is X,, where N= min{k? 1;Xk>A}.

Set a = Pr(X, > A) and M = E[X,,,].

(a) Argue the equation

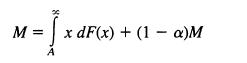
by considering the possibilities, either the first bid is accepted, or it is not.

(b) Solve for M, thereby obtaining

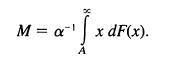
(c) When X, has an exponential distribution with parameter A, use the memoryless property to deduce M = A + A'.

(d) Verify this result by calculation in (b).

M =S xdF(x) (1)M