21. Let {x1, x2, . . . , xn} be a set of real numbers and define

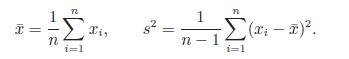
Prove that at least a fraction 1 − 1/k2 of the xi’s are between ¯x − ks and ¯x + ks.
Sketch of a Proof: Let N be the number of x1, x2, . . . , xn that fall in A = [¯x − ks, ¯x + ks]. Then

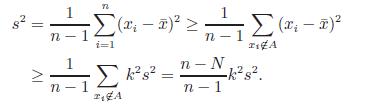
This gives (N − 1)/(n − 1) ≥ 1 − (1/k2). The result follows since N ≥ (N − 1)/(n − 1).

I = n n i=1 1 Ti, - n - ). i=1