25. Let X be a hypergeometric random variable with probability mass function

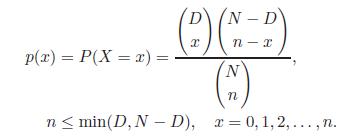
Recall that X is the number of defective items among n items drawn randomly and without replacement from a box containingD defective and N −D nondefective items.
Show that

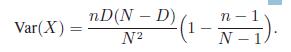
Hint: LetAi be the event that the ith item drawn is defective.Also for i = 1, 2, . . . , n, let

Then X = X1 + X2 + · · · + Xn.

p(x) = P(X = x) = (B) (-D) n-x N n nmin(D, ND), x = 0, 1, 2,..., n.