Question: 2.7. Consider a machine whose condition at any time can be observed and classified as being in one of the following three states: State 1:

2.7. Consider a machine whose condition at any time can be observed and classified as being in one of the following three states:

State 1: Good operating order State 2: Deteriorated operating order State 3: In repair We observe the condition of the machine at the end of each period in a sequence of periods. Let X denote the condition of the machine at the end of period n for n = 1, 2..... Let X0 be the condition of the machine at the start. We assume that the sequence of machine conditions is a Markov chain with transition probabilities

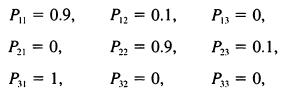
P = 0.9, P = 0.1, P3 = 0, P21 = 0,

and that the process starts in state Xo = 1.

(a) Find Pr(X4 = 1).

(b) Calculate the limiting distribution.

(c) What is the long run rate of repairs per unit time?

P = 0.9, P = 0.1, P3 = 0, P21 = 0, P22 = 0.9, P = 0.1, P = 1, P32 = 0, P = 0,

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

7. (16 marks) Consider a machine whose condition at any time can be classified as being in one of the following three states: State 1: Good operating order State 2: Deteriorated operating order State...

4.2.7 Consider a machine whose condition at any time can be observed and classified as being in one of the following three states: State 1: Good operating order State 2: Deteriorated operating order...

Consider a machine whose condition at any time can be classified as being in one of the following three states: State 1: Good operating order State 2: Deteriorated operating order State 3: In repair...

7. (16 marks)Consider a machine whose condition at any time can be classified as being in one of the following three states: State 1: Good operating order State 2: Deteriorated operating order State...

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

I have attached the corresponding lessons for assignment 8, it usually includes practice problems at the bottom that look similar to the assignment. ASSIGNMENT 7 JOB ORDER COSTING Directions: After...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Two clocks at the ends of a train are synchronized with respect to the train. If the train moves past you, which clock shows the higher time?

Maraston Marble Corporation is considering a merger with the Conroy Concrete Company. Conroy is publicly traded company, and its beta is 1.30. Conroy has been barely profitable, so it has paid an...

A stock with a P / E of 2 0 and a PEG of 2 must have a higher expected growth rate than a stock with a P / E of 2 0 and a PEG of 4 . True False

In this exercise, assume that we are considering enhancing a machine by adding vector hardware to it. When a computation is run in vector mode on the vector hardware, it is 10 times faster than the...