30. Let f(x, y) be the joint probability density function of two continuous randomvariables;

f is called circularly symmetrical if it is a function of √x2 + y2, the distance of (x, y)

from the origin; that is, if there exists a function ϕ so that f(x, y) = ϕ(√x2 + y2 ).

Prove that if X and Y are independent random variables, their joint probability density function is circularly symmetrical if and only if they are both normal with mean 0 and equal variance.

Hint: Suppose that f is circularly symmetrical; then

Differentiating this relation with respect to x yields

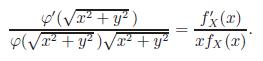
This implies that both sides are constants, so that

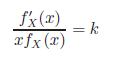
for some constant k. Solve this and use the fact that fX is a probability density function to show that fX is normal. Repeat the same procedure for fY .

fx(x)fy (y)=4(x + y).