Question: 3.4.19 Computer Challenge. Let N be a positive integer and let Z1; : : : ;ZN be independent random variables, each having the geometric distribution

3.4.19 Computer Challenge. Let N be a positive integer and let Z1; : : : ;ZN be independent random variables, each having the geometric distribution

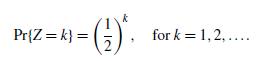
k Pr(Z = k) = (2) (-2). for k = 1, 2,....

Since these are discrete random variables, the maximum among them may be unique, or there may be ties for the maximum. Let pN be the probability that the maximum is unique. How does pN behave when N is large? (Alternative formulation: You toss N dimes. Those that are heads you set aside; those that are tails you toss again. You repeat this until all of the coins are heads. Then, pN is the probability that the last toss was of a single coin.)

k Pr(Z = k) = (2) (-2). for k = 1, 2,....

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

4.19. Computer Challenge. Let N be a positive integer and let Z . . . , Z be independent random variables, each having the geometric distribution Since these are discrete random variables, the...

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

I can't wait to rate!!!!! Since computer A's address isn't already in the table, the switch will record the address of computer A. Since Computer B's address in not in the table, the switch will...

Content Bb 21051217 C learn-us-east-1-prod-fleet02-xythos.content.blackboardcdn.com/5cc71db6522fe/21051217?X-Blackboard-Expiration=1634860800000&X-Blackboard-Signature=7706... To E 21051217 1 / 5 | -...

May I seek you help for the following questions about loss models application and probability, please? Thank you. Problem 3 (Required, 25 marks) (a) We let X1,X2, . ,Xn be 71 independent random...

For the following Markov models a) draw the transition diagram, if one is not provided; b) put the states in (some) order and write down the transition matrix; c) calculate the probability of the...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

MATH S350 TMA 01 Hints Question 1 Let A and B be the event that water is contaminated with excessive amount of pollutant A and pollutatnt B respectively. Remarks: 1. Half of those communities whose...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

Planning Demand and Supply in a Supply Chain Capacity Planning and Assignment 1 utdallas.edu/~metin Outline Capacity Planning Product-to-plant Assignment utdallas.edu/~metin 2 Deterministic Capacity...

Read the case study NCRCC: Teeing Up a New Strategic Direction Question 1: Build the management-research question hierarchy, through the investigative questions stage. Then compare your list with the...

Current Attempt in Progress Sheridan Company has a balance in its Accounts Receivable control account of $10,700 on January 1, 2022. The subsidiary ledger contains three accounts: Bixler Company,...

Which feature of a limited liability company is most like that of a corporation? Owners are called 'members' Federal corporate taxation rates Pass - through taxation Full limited personal liability

In this exercise, assume that we are considering enhancing a machine by adding vector hardware to it. When a computation is run in vector mode on the vector hardware, it is 10 times faster than the...