Question: 4.6. Let be a standard normal random variable. (a) For an arbitrary constant a, show that E[(e - a)+] = 4 (a) - a[1 -

4.6. Let be a standard normal random variable.

(a) For an arbitrary constant

a, show that E[(e - a)+] = 4

(a) - a[1 - 4)(a)]

(b) Let X be normally distributed with mean μ and variance cr2. Show that

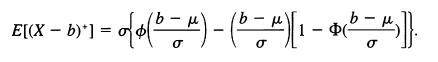
E[(x - b) - [6 ()- ( - ) [ - *

E[(x - b) - [6 ()- ( - ) [ - * )]} =

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

Q:

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Q:

Student Major 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 A M M A M M E M O A E E M A O E M A M A M A O A M E E M A M Hotel Location Cost/Night Boulders Resort &...

Q:

IOE 419 Mark S. Daskin Service Operations Management IOE Department Winter, 2017 University of Michigan Problem set 4 DUE: MONDAY - February 20, 2017 Points: 100 points total Problem 1: Babette has...

Q:

C According to Bluefin, a paym x C According to Bluefin, a paym X C Hawaii was the first state to t X Course Hero X Assessment - Probability & D X + X C...

Q:

(i) Write down the linear program relaxation for the vertex cover problem and solve the linear program. [6 marks] (ii) Based on the solution of the linear program in (b)(i), derive an integer...

Q:

MEMORIAL UNIVERSITY OF NEWFOUNDLAND DEPARTMENT OF MATHEMATICS AND STATISTICS Midterm Examination Statistics 2500 - 001 Name: Winter 2003 Student No: Set by Dr. H. Wang OFFICE USE ONLY Mark:...

Q:

Please could someone help me answer this test. Please mark the correct one in the group of alternatives. First it is in Spanish and then at the bottom it is in English. ASAP. Thanks Pregunta 1 4pts...

Q:

Please show your workings. Diane Bruns is the chairman of an enormous city. Recently, she has gotten worried about the likelihood that huge quantities of individuals who are drawing joblessness...

Q:

A seismic probe bores itself into the seabed, going as deep as it can before running out of fuel. This takes about five minutes. It rotates its spiral drill head at rate R(t) that follows a...

Q:

Can someone solve this? Exercise 1. Let (2, F, P) be a probability space. Define A E F an atom of Q if A # @ and 3 and A are the only elements in F which are subsets of A. Show that distinct atoms...

Q:

Critically evaluate the role of external auditors in addressing climate risk and sustainability. Define the boundaries of External Auditing How can External Auditors assist in addressing Climate Risk...

Q:

Dolphins and bats determine the location of their prey using echolocation (see Conceptual Question 15). If it takes for a bat to receive the ultrasonic sound wave reflected off a mosquito, how far is...

Q:

If the price of the underlying stock is less than the strike price, the put option is said to be

Q:

In this exercise, assume that we are considering enhancing a machine by adding vector hardware to it. When a computation is run in vector mode on the vector hardware, it is 10 times faster than the...