Question: 6. Let X be a discrete random variable with the set of possible values {x1, x2, . . . , xn}; X is called a

6. Let X be a discrete random variable with the set of possible values {x1, x2, . . . , xn};

X is called a discrete uniform random variable if

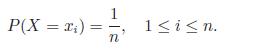
P(X=i) 1in. n

(a) Find E(X) and Var(X) for the special case, where P xi = i, 1 ≤ i ≤ n. Note that n i=1 i = n(n + 1)/2 and Pn i=1 i2 = n(n + 1)(2n + 1)/6.

(b) Let X be a random integer from the set {1, 2, . . .N}. Find E(X), Var(X), and σX.

P(X=i) 1in. n

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

Q:

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

Q:

2.1 Marginal and conditional probability: The social mobility data from Sec- tion 2.5 gives a joint probability distribution on (Y1, Y2)= (father's oc- cupation, son's occupation). Using this joint...

Q:

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

Q:

11. For n = 1, 2, 3,... , let xn = (1)nn. Let X be a discrete random variable with the set of possible values A = {xn : n = 1, 2, 3,...} and probability mass function p(xn) = P (X = xn) = 6 (n)2 ....

Q:

Let X be a discrete random variable with state space {1,2,3}, a hypothetical three sided die. Suppose that the probabilities associated with the state space are P(X = 1) = 40, == P(X = 2) = 30,...

Q:

6. Automobile Collision Claims. State Farm Insurance has developed the following table to describe the distribution of automobile collision claims paid during the past year. a. Set up a table of...

Q:

Lower End of Interval Upper End of Interval Payment($) 0 0.85 0 0.85 0.91 500 0.91 0.94 1,000 0.94 0.96 2,000 0.96 0.98 5,000 0.98 0.99 8,000 0.99 1 10,000 (b) Construct a simulation model to...

Q:

Mean as Center of Gravity. Let X be a discrete random variable with a finite number of possible values, say, x1, x2,..., xm . For convenience, set pk = P(X = xk ), for k = 1, 2, ..., m. Think of a...

Q:

1. Let X be a discrete random variable that may assume values x = 0; 1; 2 respectively with probabilities p1; 0:5; p2. Which values of p1 and p2 define a probability distribution? A p1 = 0.5 and p2 =...

Q:

Could you check my answer and if they are not correct answer then with an explanation please thanks so much. Question 2: Roll a Die Twice (30 marks) Roll a fair dice twice. Let X be a discrete random...

Q:

Two objects are identical except that one is hotter than the other. Compare how they respond to identical forces.

Q:

What are the advantages and implications to a society of steadily growing economy? What are the historical trends in the United States for economic growth over the last one hundred years? What...

Q:

For each of the following transactions, what is the initial effect ( increase or decrease ) oen MI ? Yoes sell a few sharcs of stock and put the proceeds into your saviser accoune. Yoe sell a few...

Q:

Draw all constitutional isomers with molecular formula C 4 H 11 N, and provide a name for each isomer.