6. Let X be a lognormal random variable with parameters and 2. By definition, lnX N(, 2). In Example 11.6, we showed that

6. Let X be a lognormal random variable with parameters μ and σ2. By definition, lnX ∼ N(μ, σ2). In Example 11.6, we showed that for any positive r,

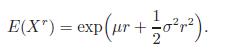
Show that even though moments of all orders of X exist, in no neighborhood (−δ, δ), δ > 0, around 0,MX(t) exists. That is, the moment-generating function of X does not exist.
Hint: Let Y = lnX; then X = eY . Show that, for any fixed t > 0, MX(t) ≥ (tn!)MY (n) for all positive integers n, and (tn!)MY (n) → ∞as n → ∞.

1 E(X") = exp(r + 20).