7.2. Consider the random walk Markov chain whose transition probability matrix is given by

The transition probability matrix corresponding to the nonabsorbing states is

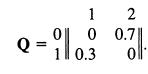
Calculate the matrix inverse to I - Q, and from this determine

(a) the probability of absorption into state 0 starting from state 1;

(b) the mean time spent in each of states 1 and 2 prior to absorption.

0 1 2 3 1 0 0 0 0.3 0 0.7 0 P = 2 0 0.3 0 0.7 3 0 0 0 1