A random variable X has the density f (x)=0 for x

for x ∈ [k,k + 1) and k = 0,1, ... . Graph f (x). What is P(k ≤ X ≤ k+1) and P(k ≤ X ≤ k+ 1/2|k ≤ X ≤ k+1)?

Show that the distribution of X coincides with the distribution of the r.v. Z +K, where the r.v.’s Z and K are independent, Z is uniform on [0,1], and K has the second version of the geometric distribution with parameter p = 1/2. Namely,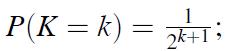

see, for example, the Appendix, Table 1. Find E{X} and Var{X}. (Advice: When considering the d.f. of X, use the formula for total probability.)