Let (left(N_{t} ight)_{t geqslant 0}) be a Poisson process with intensity (lambda=1) (see Problem 10.1 for the definition). Show that for (mathscr{F}_{t}^{N}:=sigmaleft(N_{r}: r leqslant t

Let \(\left(N_{t}\right)_{t \geqslant 0}\) be a Poisson process with intensity \(\lambda=1\) (see Problem 10.1 for the definition). Show that for \(\mathscr{F}_{t}^{N}:=\sigma\left(N_{r}: r \leqslant t\right)\) both \(X_{t}:=N_{t}-t\) and \(X_{t}^{2}-t\) are martingales. Explain why this does not contradict Theorem 19.5.

Data From Theorem 19.5

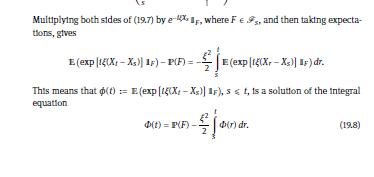
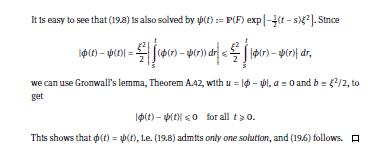
19.5 Theorem (Lvy 1948). Let (X, Ft)tao, Xo = 0, be a real-valued, adapted process Ex. 19.2 with continuous sample paths. If both (X, F)20 and (X-t, F) are martingales, Ex. 19.3 then (X) is a Brownian motion with filtration (F)120. Theorem 19.5 means, in particular, that BM is the only continuous martingale with quadratic variation (B), = t. The way we have stated Ito's formula, we cannot use it for (X)to as in Theorem 19.5. Nev- ertheless, a close inspection of the construction of the stochastic integral in Chapters 15 and 16 shows that all results remain valid if the integrator dB, is replaced by dx, where (X+)30 is a continuous martingale with quadratic variation (X), t. For Steps 2 and 3 of the proof of Theorem 18.1, cf. (18.7) and (18.8) in the proof of Lemma 18.4, we have to replace Theorem 9.1 by Corollary 9.12. In fact, Theorem 19.5 is an ex-post vindication for this since such martingales already are Brownian motions. In order not to end up with a circular conclusion, we have to go through the proofs of Chapters 15-18 again, though.