Let (sigma_{Pi}, b_{Pi} in mathcal{S}_{T}) which approximate (sigma, b in mathcal{L}_{T}^{2}) as (|Pi| ightarrow 0), and consider the It processes (X_{t}^{Pi}=X_{0}+int_{0}^{t} sigma_{Pi}(s) d B_{s}+int_{0}^{t} b_{Pi}(s)

Let \(\sigma_{\Pi}, b_{\Pi} \in \mathcal{S}_{T}\) which approximate \(\sigma, b \in \mathcal{L}_{T}^{2}\) as \(|\Pi| ightarrow 0\), and consider the Itô processes \(X_{t}^{\Pi}=X_{0}+\int_{0}^{t} \sigma_{\Pi}(s) d B_{s}+\int_{0}^{t} b_{\Pi}(s) d s\) and \(X_{t}=X_{0}+\int_{0}^{t} \sigma(s) d B_{s}+\int_{0}^{t} b(s) d s\). Adapt the proof of Lemma 18.5 to show that

\[\int_{0}^{T} g\left(X_{s}^{\Pi}ight) d X_{s}^{\Pi} \xrightarrow[|\Pi| ightarrow 0]{\mathbb{P}} \int_{0}^{T} g\left(X_{s}ight) d X_{s} \quad \text { for all } g \in \mathcal{C}_{b}(\mathbb{R})\]

Data From Leema 18.5

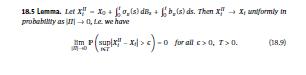
18.5 Lomma. Let X-Xo+(s) dB, + b,(s) ds. Then x X, uniformly in probability as II Q, Le. we have m P (sup>)-0 for all 0, T> 0. (18.9)