Question: Let X be a random variable with the probability density function Prove that E ???? |X| converges if 0 f(x) = 1 (1+x)' -x <

Let X be a random variable with the probability density function

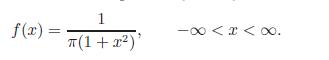
f(x) = 1 (1+x)' -x < x < .

Prove that E ????
|X|α
converges if 0

f(x) = 1 (1+x)' -x < x < .

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

Q:

PLEASE ANSWER ALL QUESTIONS 3.105. Let X be a random variable that can take on the values 2, 1, and 3 with respective probabilities 1 3, 1 6, and 1 2. Find (a) the mean, (b) the variance, (c) the...

Q:

CASE STUDY: HEAVY-TAILED DISTRIBUTION AND REINSURANCE RATE-MAKING The purpose of this case study is to give a brief introduction to a heavytailed distribution and its distinct behaviors in contrast...

Q:

nodes, but at least its bias can be quantified by Markov Chain L. INTRODUCTION analysis and thus can be corrected via appropriate re-weighting The popularity of online social networks (OSNs) in...

Q:

11 Let X be a random variable with the probability density function f(x) 1 (1+x)' Prove that E(X) converges if 0

Q:

9. Let X be a random variable with the probability density function given by Let Find the probability density function of Y . f(x) = Se- { 0 if x 0 elsewhere.

Q:

12. For an integer n 3, let X be a random variable with the probability density function f (x) = 0 *n + 1 2 , n 0*n 2 , * 1 + x2 n ,(n+1)/2 ,

Q:

11. Let X be a random variable with the probability density function f (x) = 1 (1 + x2) ,

Q:

7 pt Let X be a random variable with the probability density function (PDF) C(1m2) 1 0.5? ) (e 2 pt What are the mean and the variance of X

Q:

8. Let X be a random variable with the probability density function given by f (x) = B ex if x 0 0 elsewhere. Let Y = X if X 1 1/X if X > 1. Find the probability density function of Y .

Q:

8. Let X be a random variable with the probability density function (X is called a Cauchy random variable.) Find the probability density function of Z = arctanX. f(x) = 1 (1+x)'

Q:

Solve the Bernoulli equation in problems. a. y' + ty = ty3 b. y' - y = ety2

Q:

1) Medical Decisions: Suppose that you performed a small clinical trial of patients that need blood thinners. There were 60 people in each group. You tested Aspirin ($10.00/mo) against the pharma...

Q:

The following investment has a 14.5% required return and the following cash flows. Based on the profitability index rule, should you accept this project? Year Cash Flow Year 0 -$46,500 Year 1 $12,200...

Q:

On a planet in a different solar system the acceleration of gravity is greater than it is on Earth. If you float in a pool of water on this planet, do you float higher than, lower than, or at the...