Question: Let (X(t), Y(t)) be any two stochastic processes. Show that (X(u1),..., X(up)) (Y(u),..., Y(up)) for all u 1 implies (X(S1),..., X(Sn)) (Y(t),..., Y(tm)) for all

Let \(X(t), Y(t)\) be any two stochastic processes. Show that

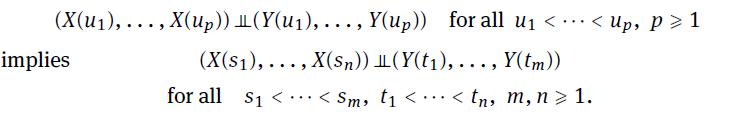
(X(u1),..., X(up)) (Y(u),..., Y(up)) for all u 1 implies (X(S1),..., X(Sn)) (Y(t),...,

(X(u1),..., X(up)) (Y(u),..., Y(up)) for all u 1 implies (X(S1),..., X(Sn)) (Y(t),..., Y(tm)) for all s < < Sm, t < ... < tn, m, n 1.

Step by Step Solution

★★★★★

3.49 Rating (149 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

Q:

Q1. You have identified a market opportunity for home media players that would cater for older members of the population. Many older people have difficulty in understanding the operating principles...

Q:

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

Q:

s1 educated (SSE) student for every three public school educated (PSE) students. Reasoning that students are not very dissimilar from threads, he suggests the following entry and exit routines be...

Q:

marks Ito calculus 3 marks Let X t and Y t be two stochastic processes such that dX x X t t dt ox X t t dZx dY uy Y t t dt oy Y t t dZy Xi 1 Xi Yi 1 Yi with dZx t dzy t being the increments for two...

Q:

the green line is a question. thank you Consider a standard binomial model of a risky asset where there are two states of nature, the UP state and the DOWN state. The former is denoted by U and the...

Q:

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

Q:

Recall that N is the set of positive integers and Q is the set of rational numbers. NOTE: "Limit point\Sequences - Part 2 (Week 4) Infinite Limits Definition. A sequence (sn) is said to diverge to +...

Q:

MUST BE CORRECT ANSWERS A small software company has the following simplified cashflow, funded by shareholders' equity of 20,000 and a bank overdraft of 5000: Invoiced money received 2 months after...

Q:

1. (60 pts True/False. Indicate whether the statement is true or false. If the statement is false, present an explanation or counterexample. (No explanation necessary for each true statement.) (2...

Q:

4 This assignment, based on the content of Unit 4 of the Study Guide, is worth 3% of your grade. We recommend that you hand it in after you complete Unit 4. You must show all of your work in order to...

Q:

READ THE SCENARIO BELOW AND ANSWER THE QUESTIONS THAT FOLLOW. The ABC International Bank which is a banking organisation headquartered in South Africa and with operating branches in all the nine...

Q:

Corporation A was involved in merger discussions with Corporation B. During this time, Corporation A made public statements denying that any merger negotiations were taking place or that it knew of...

Q:

Within a business sector, average long - term debt - to - equity ratios are typically a . similar. b . equal. c . wide ranging. d . unknown except for a few individual businesses.

Q:

Why the performance of savings institutions deteriorated in the 1980s? AppendixLO1

Q:

In Bridge, fifty-two cards are dealt to four players, thirteen to each. (a) Write a formula for p 1 , the probability that a particular player, say, the first, will get a whole suit (all thirteen...

Q:

Similar to Example 2.2-7c, prove that the probability of selecting a red ball at any draw is the same as at the first draw. Example 2.2-7c There are exactly two participants in a contest that...

Q:

You select at random k numbers from the sequence 1, ...,n. Show that the probability that you will choose a particular combination of numbers, say, 1,2, ...,k, is 1/ (n k). Suppose that now you...

Q:

this stock? Multiple Choice 17.28% 17.78% 18.72% 3.00% 16.04%

Q:

You have been hired as a consultant for Pristine Urban-Tech Zither, Incorporated (PUTZ), manufacturers of fine zithers. The market for zithers is growing quickly. The company bought some land three...

Q:

The fixed overhead spending variance is also called the ________ variance. a. production volume b. fixed overhead usage c. fixed overhead efficiency d. fixed overhead flexible budget