Question: Prove that rigorously, and give a combinatorial interpretation. Proceeding from (4.1), show that all combinations (n k) can be arranged in the triangle below, which

Prove that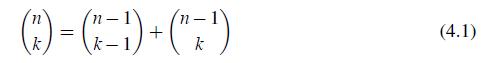 Prove thatrigorously, and give a combinatorial interpretation. Proceeding from (4.1), show that

rigorously, and give a combinatorial interpretation. Proceeding from (4.1), show that all combinations (n k) can be arranged in the triangle below, which is constructed in the following way. We start with one in the first row as is shown below, and then, moving down, add two adjacent numbers and write the sum directly underneath. (An empty position is treated as zero.) In other words, each number in the Pascal’s triangle is the sum of the two numbers above it. It helps counting combinations.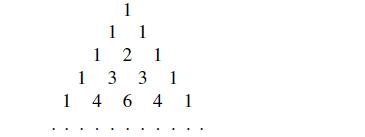 all combinations (n k) can be arranged in the triangle below, which

Step by Step Solution

★★★★★

3.31 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We may divide all combinations of k elements selected from n elements into two groups those that c... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Probability And Stochastic Modeling Questions!

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

Sidhu v. Canada (Citizenship and Immigration), 2012 FC 515 (CanLII) [1] This is an application undersubsection 72(1) of the Immigration and Refugee Protection Act , SC 2001, c. 27 (Act) for judicial...

I need to see the SPSS output. You need to have all z-scores, all charts, all descriptives data from SPSS, everything you used to answer the questions. I am sending you what the previous tutor sent...

07-Bickman-45636:07-Bickman-45636 7/28/2008 6:13 PM Page 214 CHAPTER 7 Designing a Qualitative Study Joseph A. Maxwell T raditionally, works on research design (most of which focus on quantitative...

MAT 243 Online Written Homework Assignments for Week 3 (units 6-9) 1. Prove or disprove: = [1,3) (2,3] is the empty set. 2. Prove that if A and B are sets, . Your proof must be based on the exact...

6. Optional extra credit: trophy testing. (This is a good problem for those who want a challenge. It will be graded with high standards and not much partial credit, and no regrades will be done.)...

3) Improper and proper Priors (20 Pts.) Explain whether the following can be turned into proper priors and their individual usefulness. You do not need to rigorously prove your answer but give...

You select at random k numbers from the sequence 1, ...,n. Show that the probability that you will choose a particular combination of numbers, say, 1,2, ...,k, is 1/ (n k). Suppose that now you...

Following is a data set that contains two attributes, X and Y, and two class labels, "+" and "". Each attribute can take three different values: 0, 1, or 2. The concept for the "+" class is Y = 1 and...

Write and balance the chemical equation described by Exercise 2. In exercise 2, from the statement sodium metal reacts with water to produce sodium hydroxide and hydrogen, identify the reactants and...

2. The demand for an item is 250 units per week. The set-up cost is Rs 1000 per cycle. The production rate for the item is 600 units per week. The inventory carrying cost is Re 0.30 per unit per...

For what types of products would the initial focus of the concept generation activity be on the form and user interface of the product and not on the core technology? Describe specific examples. Q-968

Let $\left(B_{t}, \mathscr{F}_{t} ight)_{t \geqslant 0}$ be a $\mathrm{BM}^{1}$ such that $\mathscr{F}_{0}$ contains all measurable null sets and let $\tau$ be a stopping time. Show that...

Assume that the processes in Lemma 5.7 or in Lemma 5.8 are only "almost surely right continuous", resp. "almost surely continuous". Identify all steps in the proofs where this becomes relevant and...

Let $\left(\mathscr{F}_{t} ight)_{t \geqslant 0}$ be an admissible filtration for the Brownian motion $\left(B_{t} ight)_{t \geqslant 0}$. Mimic the proof of Lemma 2.14 and show that for each...

Hello, Please provide me the ans of J,K and L thank you. solve keon has asked meena about pricing..... Since Meena hasn't advertised very heavily (she currently pays $300 a month for advertising on...

A company reported a gross profit percentage of 25% with net sales of $347,800. What is the amount of cost of goods sold? Multiple Choice O $86,950 0 $108,688 0 $326,063 0 $260,850

language is python In this problem we will implement the Shortest Path Algorithm that we discussed in the class. You have to write Python program that implements the algorithm discussed in the class...