The continuous random variable \(X\) is uniformly distributed on \([0,2]\).

(1) Draw the graph of the function

\[p(\varepsilon)=P(|X-1| \geq \varepsilon)\]

in dependence of \(\varepsilon, 0 \leq \varepsilon \leq 1\).

(2) Compare this graph with the upper bound for the probability

\[P(|X-1| \geq \varepsilon)\]

given by the Chebyshev inequality, \(0 \leq \varepsilon \leq 1\).

(3) Try to improve the Chebyshev upper bound for

\[P(|X-1| \geq \varepsilon)\]

by the Markov upper bound (5.8) for \(a=3\) and \(a=4\).

Data from 5.8

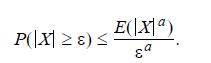
P(|X| ) E(Xa)