Under otherwise the same assumptions as made in example 7.10, determine the ruin probability if the random claim size \(M\) has density

\[b(y)=\lambda^{2} y e^{-\lambda y}, \lambda>0, y \geq 0\]

This is an Erlang-distribution with parameters \(\lambda\) and \(n=2\).

Data from Example 7.10

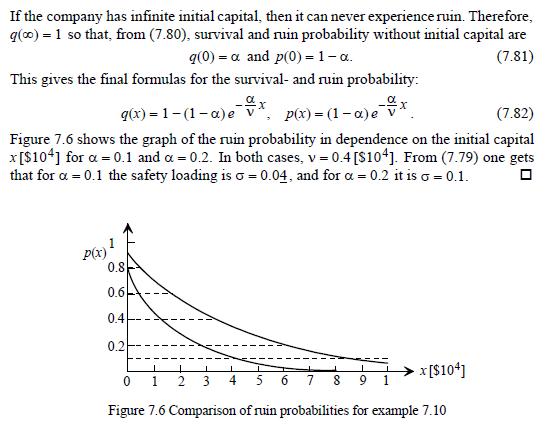
Example 7.10 Let the claim size M have an exponential distribution with mean value E(M) v. Then M has density = b(y) = e-/v, y 0, so that b(s)=e-sye(1/v)y dy = : 1 vs+1 Inserting (s) in (7.78) gives the Laplace transform of the survival probability: (s) = vs+1 s (vs+1)-vs 4(0) . By introducing the coefficient - 0 < x < 1, (7.79) (s) simplifies to 1 1 1 = + vs s+a/v ] 9(0). (s)[ Retransformation yields (Table 2.5, page 105) 1 g(x) + ) =[e-%x + U-Je-%x]q(0). (7.80)