ANOVA with equal weights. Consider the model of the analysis of variance for s groups with respective expectations mi and sample sizes ni . Let em D 1 s

Ps iD1 mi be the averaged effect of all groups, and ˛i D mi em the additional effect of the i th group. (In the unbalanced case when ni does depend on i , em differs from the overall mean m introduced in (12.30).)

Show the following:

(a) The estimator eM D 1 s

Ps iD1Mi (which is, in general, different from M) is a best linear unbiased estimator of em, and O ˛i D Mi eM is a best linear unbiased estimator of ˛i .

(b) For every parameter .m; v/ 2 Rs 0;1OE , the variances are given by

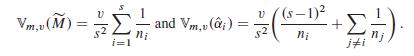
(c) If k 2 N and n D sk, then Vm;v.eM/ is minimal for the sample sizes n1 D Dns D k.
On the other hand, if n D 2.s1/k, then Vm;v. O ˛i / is minimal whenever ni D .s1/k and nj D k for j ¤ i .

Vm,v(M) (s-1) -). ji and Vm,v (i) ni $2 ni