Question: Dirichlet and multinomial distributions. As a generalisation of Example (7.36), consider an urn model in which each ball has one of a finite number s

Dirichlet and multinomial distributions. As a generalisation of Example (7.36), consider an urn model in which each ball has one of a finite number s of colours (instead of only two).

Let ‚ be the set of all probability densities on ¹1; : : : ; sº. Suppose that the prior distribution

˛ on ‚ is the Dirichlet distribution D for some parameter 2 0;1OEs , which is defined by the equation

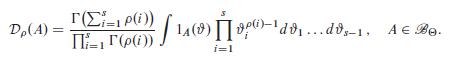
DP(A) = (14) 9-18, ... s-1, A Bo (1 (1) ((1) i=1

Here, the integral runs over all .#1; : : : ; #s1/ for which # WD .#1; : : : ; #s1; 1
Ps1 iD1 #i /
belongs to ‚. The fact that D is indeed a probability measure will follow for instance from Problem 9.8. (In the case 1, D is the uniform distribution on ‚.) We take a sample of size n with replacement. For each colour composition # 2 ‚, the colour histogram then has the multinomial distributionMn;#. Determine the associated posterior distribution.

DP(A) = (14) 9-18, ... s-1, A Bo (1 (1) ((1) i=1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Probability Statistics Questions!

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

1 2.3 Definition of a Discrete Probability Function Definition: Let S be a discrete sample space from some experiment. A function P, defined on all events in S, is said to be a probability function...

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

BE562: Problem Set 3 Fall 2016 Due 10/21/2016 8PM 1. Hidden Markov Models and Protein Structure (20 pts) One biological application of hidden Markov models is to determine the secondary structure...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

Data gistrun sending inside a pack fills in as conventional allowing subordinate rules to execute on progressive clock cycles. Correspondence between gatherings conventionally causes a surprising...

For monotone functions f, f0: P Q between posets (P, vP ) and (Q, vQ), let f v f(i) Prove that the binary relation v is a partial order. [3 marks] (ii) For monotone functions between posets p : P 0...

4.10 Suppose that the probabilities {i, 1 i t} of a multinomial distribution depend on the parameter vector = (1,...,d). Show that the expected information matrix for is given by: J = mD r1D,...

Just as the binomial distribution is a special case of a much more general principle in algebra (the binomial expansion), so the multinomial distribu tion is a special case of another quite general...

Compare and contrast the following pairs of distributions with 3 differences foreach: Chi-square vs normal distributions Hyper-geometric vs multinomial distributions Student t vs Fisher-Snedecor...

If savers dont feel safe putting their money in banks or buying bonds, whats the best way to sum up whats happening in the market for loanable funds? a. Supply of savings falls and the interest rate...

2. Western Airlines merged with a smaller airline recently. Every day since the merger, a random sample of 30 Western flights has been analyzed every day. A flight that takes off more than 10 minutes...

10. (True/False): In current 64-bit chip implementations, all 64 bits are used for addressing.

For each of the following cases, identify the rejection region that should be used to test H0: 21 = 22 against Ha: 21 > 22. Assume v1 = 30 and v2 = 20. a. = .10 b. = .05 c. = 025 d. = .01