Error propagation for transformed observations. Let .Xi /i1 be a sequence of i.i.d.

random variables taking values in a (possibly unbounded) interval I R, and suppose the variance v D V.Xi/ > 0 exists. Let m D E.Xi / and f W I ! R be twice continuously differentiable with f 0.m/ ¤ 0 and bounded f 00. Show that

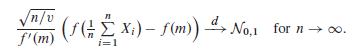
Hint: Use a Taylor’s expansion of f at the point m and control the remainder term by means of Chebyshev’s inequality.

n/v m)(xi) - f(m)) No.1 for n.