Question: Prove that the gamma function G(a)= R 0 xa????1e????x dx, a >0 fulfills the equalities G(1) = 1, G(1=2) = p p, and G(a

Prove that the gamma function G(a)=

R ¥

0 xa????1e????x dx, a >0 fulfills the equalities G(1) = 1, G(1=2) =

p p, and G(a +1) = aG

(a) for any a > 0. Deduce the two formulas

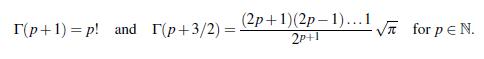
(2p+1)(2p-1)...1 T(p+1) p! and (p+3/2)= 2P+1 for pN.

(2p+1)(2p-1)...1 T(p+1) p! and (p+3/2)= 2P+1 for pN.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Probability Statistics Questions!

Q:

1.6.2 Volume of a p-Dimensional Ball We will prove the Formula (1.1) for the volume Vp(r) of a p-dimensional ball of radius r > 0. 1. Prove that the gamma function G(a)= R 0 xa????1e????x dx, a >0...

Q:

5. /16 pts) A particle in a one-dimensional, infinite square well of length L has the initial, normalized wave function CO I (x, 0) = (a) (8 pts) Find I(x, t). (b) (4 pts) What is the probability of...

Q:

Note: All ML code must be explained clearly (INJAVAXX)and should be free of needless complexity. 2 CST.2016.1.3 2 Foundations of Computer Science Please help. (2c) (a) A prime number sieve is an...

Q:

I need it in JAVAx Objects: Electronic health records (EHRs) in a nationwide service. Policy: The owner (patient) may read from its own EHR. A qualified and employed doctor may read and write the EHR...

Q:

: (i) What data structures are maintained by the page manager. (ii) What happens when a machine performs a read operation to a page. (iii) What happens when a machine performs a write operation to a...

Q:

llustrate different ways of connecting these components together to span a range of performance requirements. [10 marks] For each of the performance categories that you identify state today's typical...

Q:

QUESTION 15. [7 points] Find. 2 ) HINT: split in 3 fractions, make every fraction a POWER, and then use power rule for integrals (along with sum, constant term rules). As an example: the first term...

Q:

Kindly give only correct answers showing your steps 1. (a) Use the Intermediate Value Theorem to show that the equation - sin (x) + sin(x) =-1 has at least two distinct real solutions on (0, ce)....

Q:

Consider the simple MDP shown below. Starting from state s 1 , the agent can move to the right ( a 0 ) or left ( a 1 ) from any state si . Actions are deterministic ( e . g . choosing a 1 at state s...

Q:

This is my question, thankyou 1. Suppose f : A - A such that f of is bijective. Is f necessarily bijective? 2. Suppose that f : A - B is a surjective and Y C B. Show that f ( f -] ( Y ) ) = Y. 3. Let...

Q:

Briefly discuss what this paired trade suggests to you about the manager's implied view as to: (1) The general direction of future interest rate movement, (2) The future shape of the par yield curve,...

Q:

Prepare a statement of owners equity and a classified balance sheet from the worksheet for Johns Company in Figure. (Of the Mortgage Payable, $220 is due within oneyear.) JOHN'S COMPANY WORKSHEET FOR...

Q:

Which of the following terms identify a type of employer ( not employee ) contribution to a 4 0 1 ( k ) plan? ( 1 ) Salary reduction ( 2 ) Formula matching ( 3 ) Discretionary matching ( 4 ) Pure...

Q:

Liquid octane (C8H18) enters a steady-flow combustion chamber at 25oC and 1 atm at a rate of 0.25 kg/min. It is burned with 50 percent excess air that also enters at 25oC and 1 atm. After combustion,...