S Autoregressive model. To describe a time evolution with deterministic growth and random errors, one often uses the following autoregressive model (of order 1):

Xk D Xk1 C p

v k; 1 k n :

Here, 2 R andv > 0 are unknown parameters, X0; : : : ; Xn the observations, and 1; : : : ; n are independent random errors with E.k/ D 0, V.k/ D 1.

(a) Introduce an appropriate expression for the mean squared error and find the least squares estimator of .

(b) Let X0 D 0 and suppose the error variables k are standard normally distributed. Show that the likelihood function of the model is given by

;v D .2v/

n=2 exp h

Pn kD1

.Xk Xk1/2=2v i

:

(c) Consider the test problem H0 W D 0 (‘no dependence’) against H1 W ¤ 0. Show that, under the assumptions of part (b), the likelihood ratio is a monotone function of the modulus of the sample correlation coefficient

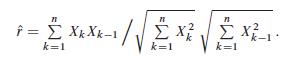
# = -1 k=1 k=1 k-1 k=1