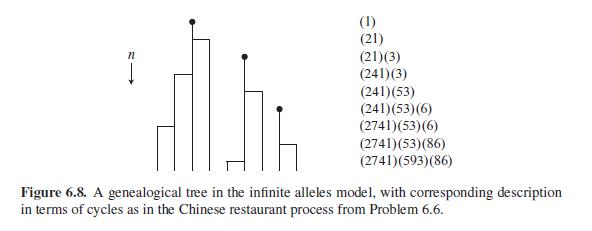
S Hoppe’s urn model and Ewens’ sampling formula. Imagine a gene in a population that can reproduce and mutate at discrete time points, and assume that every mutation leads to a new allele (this is the so-called infinite alleles model). If we consider the genealogical tree of n randomly chosen individuals at the times of mutation or birth, we obtain a picture as in Figure 6.8. Here, every bullet marks a mutation, which is the starting point of a new ‘clan’

of individuals with the new allele. Let us now ignore the family structure of the clans and only record their sizes. The reduced evolution is then described by the following urn model introduced by F. Hoppe (1984).

Let# > 0be a fixed parameter that describes the mutation rate. Suppose that at time 0 there is a single black ball with weight # in the urn, whereas outside there is an infinite reservoir of balls of different colours and weight 1. At each time step, a ball is drawn from the urn with a probability proportional to its weight. If it is black (which is certainly the case in the first draw), then a ball of a colour that is not yet present in the urn is put in. If the chosen ball is coloured, then it is returned together with another ball of the same colour. The number of

balls in the urn thus increases by 1 at each draw, and the coloured balls can be decomposed into clans of the same colour. The size distribution of these clans is described by a sequence of the form x D .xi /i1, where xi specifies the number of clans of size i . The total number of coloured balls after the nth draw is N.x/ WD P i1 i xi D n. Formally, the model is described by the Markov chain .Xn0 with state space E D ¹xD.xi /i1 W xi 2 ZC; N.x/

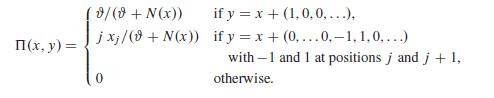
(The first case corresponds to drawing a black ball, the second to drawing a coloured ball from one of the xj clans of size j , so that the size of this clan increases to j C1.) Let 0 D .0; 0; : : : /
be the initial state, in which the urn does not contain any coloured balls.

(a) Show by induction on n 1 for arbitrary x 2 E with N.x/ D n:

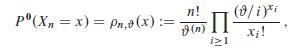
where #.n/ WD #.# C1/ : : : .# Cn1/. Hence, n;# is the size distribution of the clans of a random sample of n individuals from a population with mutation rate #. This is the sampling formula by W. J. Ewens (1972).

(b) Verify that n;# has a conditional Poisson structure as follows. If Y D .Yi /i1 is a sequence of independent random variables with Poisson distributions P ı Y 1 i D P#=i , then n;#.x/ D P.Y D xjN.Y / D n/.

(1) (21) (21)(3) (241)(3) (241)(53) (241)(53)(6) (2741)(53)(6) (2741)(53)(86) (2741)(593)(86) Figure 6.8. A genealogical tree in the infinite alleles model, with corresponding description in terms of cycles as in the Chinese restaurant process from Problem 6.6.