S Markov chains in continuous time. Let E be countable and G D .G.x; y//x;y2E a matrix satisfying the properties

(i) G.x; y/ 0 for x ¤ y,

(ii) a.x/ WD G.x; x/

(iii) a WD supx2E a.x/

We construct a Markov process .Xt /t0 that ‘jumps with rate G.x; y/ from x to y’ by using the stochastic matrix

….x; y/ D ıxy C G.x; y/=a ; x; y 2 E:

Suppose that for x 2 E we are given F a Markov chain .Zk/k0 on E with starting point x and transition matrix …, and F a Poisson process .Nt /t0 with intensity a independent of the Markov chain;

these can be defined on a suitable probability space . ;F; Px/. Let Xt D ZNt for t 0 and prove the following:

(a) For all t 0, Xt is a random variable, and

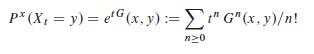
for all x; y 2 E. Note that the right-hand side is well defined since jGn.x; y/j .2a.
Conclude in particular that d dt Px.Xt D y/jtD0 D G.x; y/.

(b) .Xt /t0 is a Markov process with transition semigroup …t WD etG, t 0. By definition, this means that

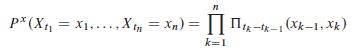
for all n 1, 0 D t0

(c) Let T
0 D 0, Z
0 D x and, recursively for n 1, let T
n D inf¹t > T
n1 W Xt ¤ Z
n1 º
be the time and Z
n D XT
n the target of the nth jump of .Xt /t0. Then, F the sequence .Z
n0 is a Markov chain on E with starting point x and transition matrix ….x; y/ D ıxy C G.x; y/=a.x/, F conditional on .Z
n0, the holding times T
nC1 T
n in the states Z
n are independent and exponentially distributed with respective parameters a.Z
n/, n 0.
Hint: Recall the construction (3.33) and combine the Problems 6.3, 3.20 and 3.18.
.Xt /t0 is called the Markov chain on E in continuous time with infinitesimal generator G, and .Z
n0 the embedded discrete jump chain.

Px (X = y) = eG (x, y) = "G" (x, y)/n!