Question: Suppose X 1 , . . . , X n is an independent sequence of exponential random variables with parameter Î» = 1. Let Z

Suppose X₁, . . . , X_nis an independent sequence of exponential random variables with parameter Î» = 1. Let

Z = max(X₁, . . . , X_n) ˆ’ log n.

(a) Show that the cdf of Z is

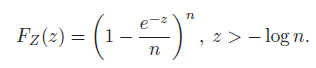
Fz(e) = (1-) Fz(2) = , 2 > - log n.

(b) Show that for all z, 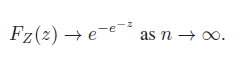Fz(2) → e-e-² as n → oo.

The limit is a probability distribution called an extreme value distribution. It is used in many fields which model extreme values, such as hydrology (intense rainfall), actuarial science, and reliability theory.

(c) Suppose the times between heavy rainfalls are independent and have an exponential distribution with mean 1 month. Find the probability that in the next 10 years, the maximum time between heavy rainfalls is greater than 3 months in duration.

Fz(e) = (1-) Fz(2) = , 2 > - log n. Fz(2) e-e- as n oo.

Step by Step Solution

★★★★★

3.48 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a For z logn F Z z PZ z PmaxX 1 X n lognz PmaxX 1 X n z logn P... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Probability With Applications Questions!

X1,... ,Xn is an iid sequence of exponential random variables, each with expected value 5. (a) What is Var[M9(X)], the variance of the sample mean based on nine trials? (b) What is p[X1 > 7], the...

Let X and Y be independent exponential random variables with parameter = 1. Simulate P(X/Y

Two servers A and B in a fast-food restaurant each start their first customers at the same time. After finishing her second customer, A notices that B has not yet finished his first customer. A then...

* 18. Let X 1 and X 2 be independent exponential random variables, each having rate LL. Let X) = minimum(X1, X2) and X(2) = maximum(X1, X2) Find (a) E[X(1)], (b) Var[X(1)], (C) E[X(2)], (d) Var[X(2)]

Can anyone help me? Suppose X 1, X 2, , X1,1 are independent exponential random variables with rates 21,12, , A\" respectively. That is, the probability function of X is, Atel\

BA 1605: Midterm Recap (Due: Feb. 27, 2015) Name _____________________________ 50 Student ID _____________________________ Section 01B 10:00~11:20 am Section 02B 01:00~02:20 pm [Questions 4 ~ 7] The...

LAB ACTIVITY #3 For each part of this lab, SUBMIT your solution to everything asked in BOLD RED in Problems 1-6 below. Include the respective R code and output. Part 1 (Continuous Distributions in R)...

May I seek you help for the following questions about loss models application and probability, please? Thank you. Problem 1 (Required, 25 marks) (a) We let X be a non-negative continuous random...

Central Limit Theorem follows from the Crameer-Wold Device. This result states the fol- lowing. Let {b, } be a sequence of random k x 1 vectors. If A b,, converges to a normal random variable for...

1. Maximum Likelihood Estimation Consider a random variable X (possibly a vector) whose distribution (density function or mass function) belongs to a parametric family. The density or mass function...

Scintillators Pty Ltd is a company engaged in the event management for celebrities. It is a family-owned company and Joe Johnson, his wife and three adult children all own shares. Joe Johnson, a...

Clinical depression occurs in about 15% of the population. Many treatments are available. The data below are based on Hollon, Thrase, and Markowitz's study (2002) comparing psychodynamic therapy,...

Assume $ 1 will buy Can$ 1 . 2 5 6 2 while $ 1 . 1 8 6 0 will buy 1 . What is the Can$ / exchange rate? 1 = Multiple Choice Can$ . 9 4 4 1 Can$ . 9 3 4 9 Can$ 1 . 0 5 9 2 Can$ 1 . 4 8 9 9 Can$ 1 . 2...

13. An investment that allows investors to legally avoid income taxes is called a(n) .

Compute a 95% CI for the mean age? Refer to the data in Table 2.13. Regard this hospital as typical of Pennsylvania hospitals. Table 2.13: Hospital-stay data

Compute a 95% CI for the mean white blood count following admission. Refer to the data in Table 2.13. Regard this hospital as typical of Pennsylvania hospitals. Table 2.13: Hospital-stay data

Answer Problem 6.12 for a 90% CI. Refer to the data in Table 2.13. Regard this hospital as typical of Pennsylvania hospitals. Table 2.13: Hospital-stay data

Economics The following data table relates to the supply schedule of a product. Quantity Supplied Price ($ Per Unit) ( Units Per Week) 5 100 10 200 15 250 20 300 25 350 30 500 Over which of the...

IN PYTHON Write a function named "loadStateDict(filename) that takes a filename and returns a dictionary of 2-character state codes and state names. The file has four columns and they are separated...

Hercules Exercise Equipment Co. purchased a computerized measuring device two years ago for $58,000. The equipment falls into the five-year category for MACRS depreciation and can currently be sold...