In this problem we discuss the global truncation error associated with the Euler method for the initial value problem y' = f(t,y), y(t _o ) = y _o . Assuming that the functions f and f _y are continuous in a closed, bounded region R of the t _y -plane that includes the point (t _o ,y _o ), it can be shown that there exists a constant L such that If |f(t,y) - f(t, y ^- |- where (t, y) and (t, y ^- ) are any two points in R with the same t coordinate. Further, we assume that f ₁ , is continuous, so the solution (t. has a continuous second derivative.

(a) Using Eq.20 show that.

Where ? = 1 = hl and ?= max |? ⁿ (t)|/2 on t ₀ ? t ? t _n .

(b) sume that if E ₀ = 0, and if |E _n | satisfies Eq. (i) then |E _n |? ?h ² (a ⁿ -1)/( ? -1) for a ? 1. Use this result to show that.

Equation (ii) gives a bound for |E _n | in term of h, L, n and ?. Notice that for a fixed h, this error bound increases with increasing n; that is, the error bound increases with distance from the starting point t ₀ .

(c) Show that (1 +hL) ⁿ ? e ^nhL ; hence

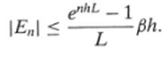
If we select an ending point T greater than t ₀ and then choose the step size h so that n steps are required to traverse the interval [t ₀ , T], then nh = T ? t ₀ , and

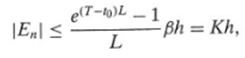
Which is Eq.25 Note that K depends on the length T - t ₀ of the interval and on the constants L and ? that are determined from the function f.

Equation (20) is below:

And Euler?s formula gives:

If we defin E _n =? (t _n ) ?y _n , then using ? ?= f(t, ? )

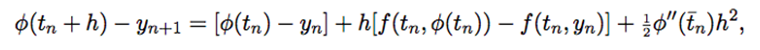
Or

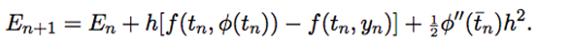
En+1] En\+h|f[ins (tn)] f (tn, Yn)] + h|p" (Tn)| \En] + h, (i) En (1+hL)" - 1 L -h. (ii) En enhL-1 L Bh. En e(T-10)L-1 L -Bh = Kh, o(tn + h) = o(tn) + '(tn)h + "(tn)h, Yn+1 = Yn+hf(tn, Yn). o(tn + h) Yn+1 = [o(tn) Yn] + h[f(tn, (tn)) f(tn, Yn)] + "(tn)h, - - En+1 = En + h[f(tn, (tn)) (tn, Yn)] + "(tn)h.