Question: Let S(n) = 1 + 2 +???..+ n be the sum of the first n natural numbers and let C(n) =13 + 23 + -

Let S(n) = 1 + 2 +???..+ n be the sum of the first n natural numbers and let C(n) =13 + 23 + - + n3 be the sum of the first n cubes. Prove the following equalities by induction on n, to arrive at the curious conclusion that C(n) = S ²(n) for every n.

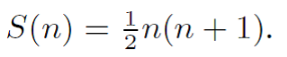
S(n) = n(n+1). C(n) = (n + 2n + n) = n(n

+ 1)

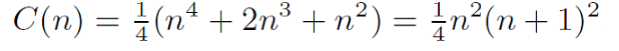
S(n) = n(n+1). C(n) = (n + 2n + n) = n(n + 1)

Step by Step Solution

★★★★★

3.32 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Inductive Proof of Sn frac12 nn 1 Base Case For n 1 S1 1 frac12 times 1 times 1 1 1 The base case ho... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Determine the sum of the first 100 natural numbers.

Find a formula for the sum of the first n terms of the sequence. Prove the validity of your formula. 9, 13, 17, 21, . . .

Find each value. a. Find the sum of the first 1000 positive integers (the numbers 1 through 1000). b. Find the sum of the second 1000 positive integers (1001 through 2000). c. Guess the sum of the...

Let S(n) = 1 + 2 + + n be the sum of the first n natural numbers and let C(n) = 1 3 + 2 3 + + n 3 be the sum of the first n cubes. Prove the following equalities by induction on n, to arrive at...

Let S(n) = 1 + 2 + + n be the sum of the first n natural numbers, and let C(n) = 13 + 23 + + n3 be the sum of the first n cubes. Prove the following equalities by induction on n: (a) S(n) = 1/2*n(n +...

Let S(n) = 1 + 2 + + n be the sum of the first n natural numbers and let C(n) = 13 + 23 + + n 3 be the sum of the first n cubes. Prove the following equalities by induction on n, to arrive at the...

3. Let S(n)=1+2++n be the sum of the first n natural numbers and let C(n)=13+ 23++n3 be the sum of the first n cubes. Prove the following equalities by induction on n, to arrive at the curious...

(a) Describe how to construct the function cpo ((D E), v) of two cpos (D, vD) and (E, vE). Prove that ((D E), v) is a cpo. (b) The function uncurry is inverse to the function curry; it takes a...

Consider the following definitions: Definition The set of linked lists of natural numbers L is defined by: Basis Step: EL Recursive Step: If I EL and n E N, then (n.) EL Definition The function...

What are the required financial statements of the U.S. government?

Best buy options with maturity on September 18, 2020 are trading with a strike of $120 (present value $119.50). The current stock price is $110, call options are trading at $1.20 and put options at...

Time Remaining 1 hour 4 4 minutes 3 4 seconds 0 1 : 4 4 : 3 4 Item 1 7 Time Remaining 1 hour 4 4 minutes 3 4 seconds 0 1 : 4 4 : 3 4 A stock can be valued by using the _ _ _ _ _ _ _ _ _ _ blank...

For the year ending December 31, 2016, the Income Statement of Saratoga Springs Company was prepared in accordance with generally accepted accounting principles. There are a number of items that the...

Q: A coil of 100 turns, having a radius of 10 cm, is placed around a very long solenoid of 1200 turns / m, having a radius of 5 cm. a. Calculate the mutual inductance of the system. b. Calculate the...

Q: A planar capacitor has two parallel armatures with an area of 53cm^2 each, separated by 4mm. There is a potential difference of 720 V between its armatures. Determine: a) The capacitance of the...

On June 30, Year 3, Franza Companys total current assets were $900,000 and its total current liabilities were $360,000 On July 1, Year 3, Franza issued a short term note to a bank for $72,000 cash...

14-2 APPLYING THE CONCEPT Global Compensation 7. I'm going overseas for a 6-month assignment, and they are paying me in the other country's currency, the euro. 8. I'm going overseas for a 6-month...

Provinces vary in their use of GST, PST, or HST systems. Question 23 options: True False

Consider a sequence of independent tosses of a coin and let P{head} be the probability of a head on any toss. Let A be the hypothesis that P{head} = a and let B be the hypothesis that P{head} = b, 0...

7.13 Let Xn, n 1 be i.i.d. random variables with some distribution with finite mean and variance 2. For every n 1, we denote Zn := n i=1 eXi 1 n . Find the almost sure limit of the sequence...

For each of the following write T (True) or F (False) : (a) All finite state space irreducible continuous-time Markov chains have a unique limiting probability distribution. (b) The counting process...

5.12 This exercise is related to Example 5.5. (i) Use the monotone function technique to prove the following inequality: ex 1 + x + x2 2 b , |x| b, where b

14. Let (Xn : n 1) be a sequence of random variables which converges in mean square. Show that E ???? [Xn Xm]2 0 as m, n . If E(Xn) = and var(Xn) = 2 for all n, show that the correlation between...

(i) Let X1,...,Xm; Y1,...,Yn be i.i.d. according to a continuous distribution F, let the ranks of the Y s be S1