Question: 0 0 Let A = 3 3 1. Compute the eigenvalues for A (list repeated eigenvalues only once) eigenvalue 1 = ; eigenvalue 2 =


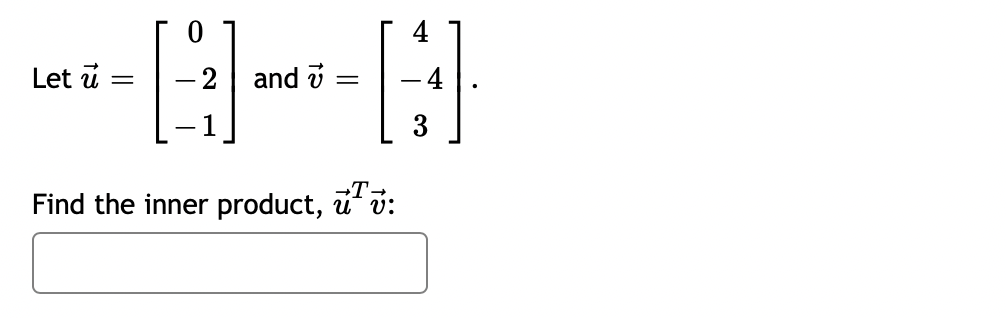



![{i=[1,4]and1_3=[5, 2] Find [:1 Find ||ii|| (Give your answer in decimal form](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6674e0d21a9a2_7616674e0d1b9f6a.jpg)
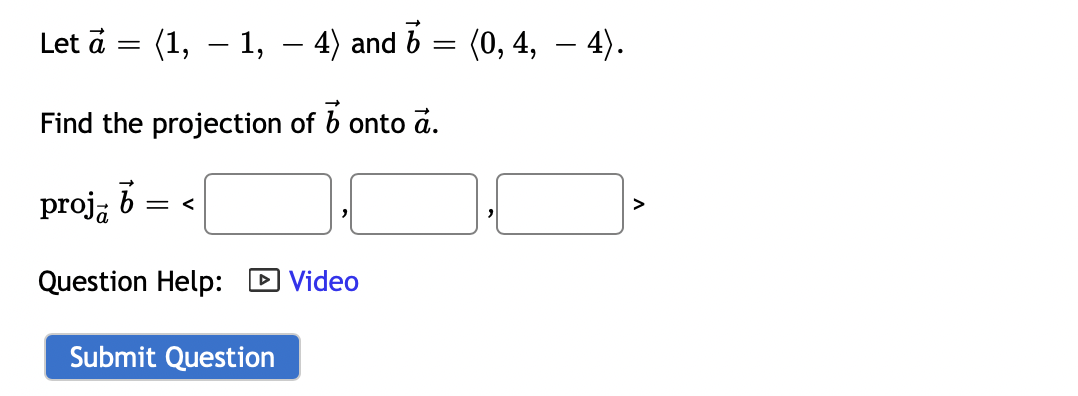






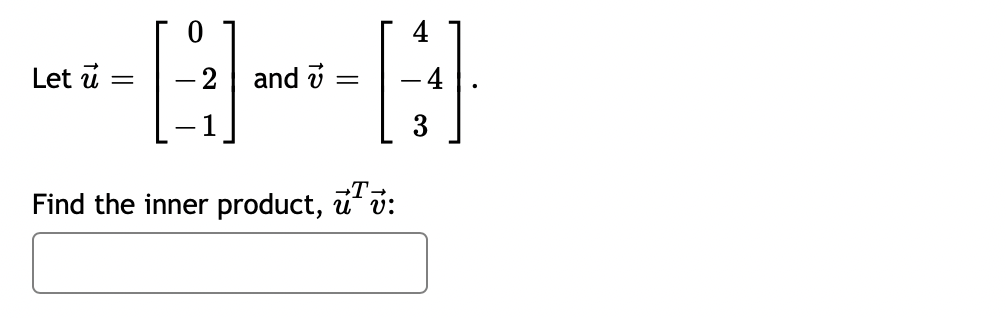

![17,. C] C] C] Let a = (1, - 1, - 4)](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6674e0d875c74_7686674e0d848297.jpg)



![[:1 C] :1 1 1 1 2 LetA: 2 1 0 and3=](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6674e0dd6e4c2_7736674e0dd3e282.jpg)

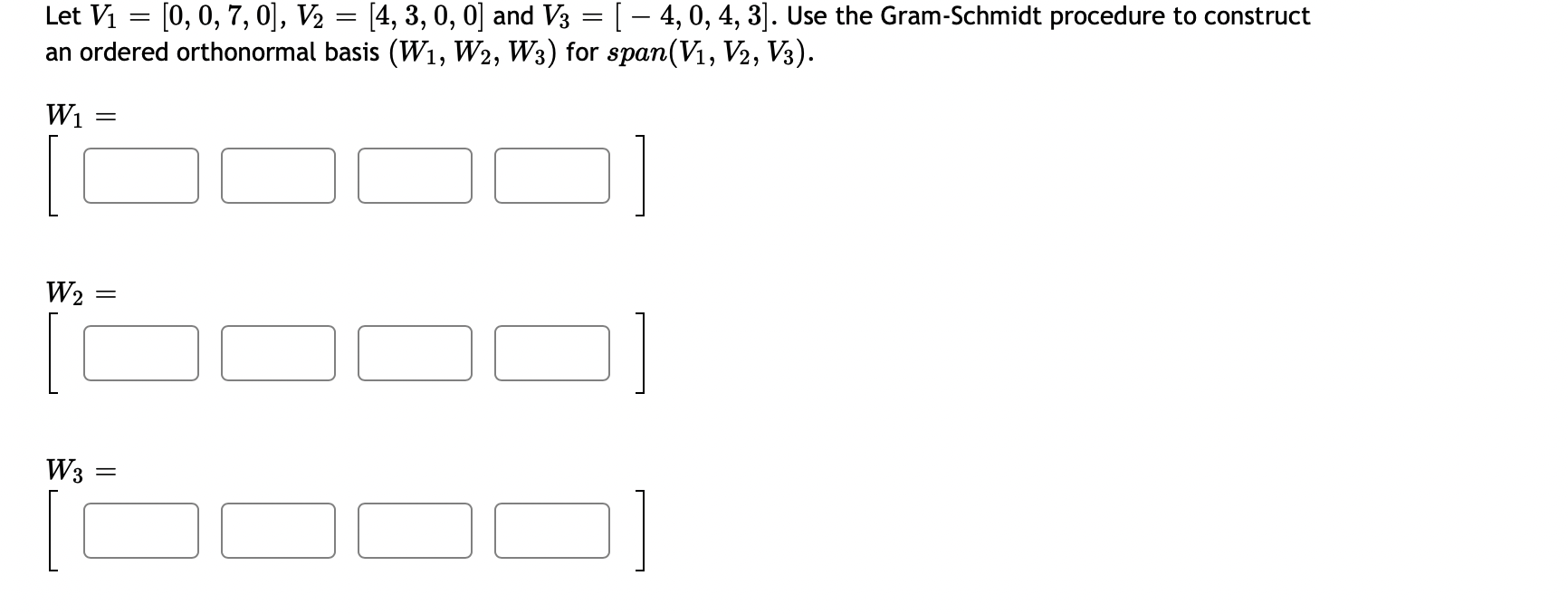
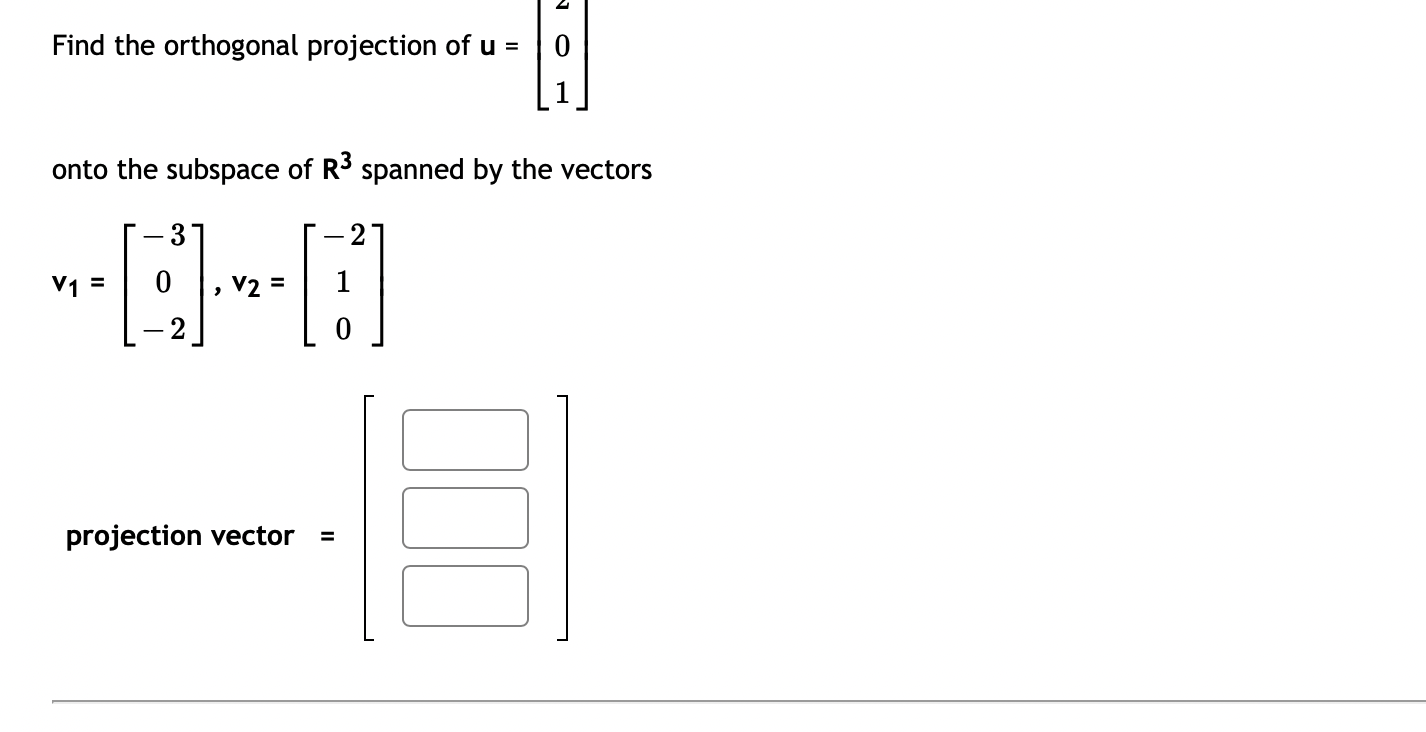
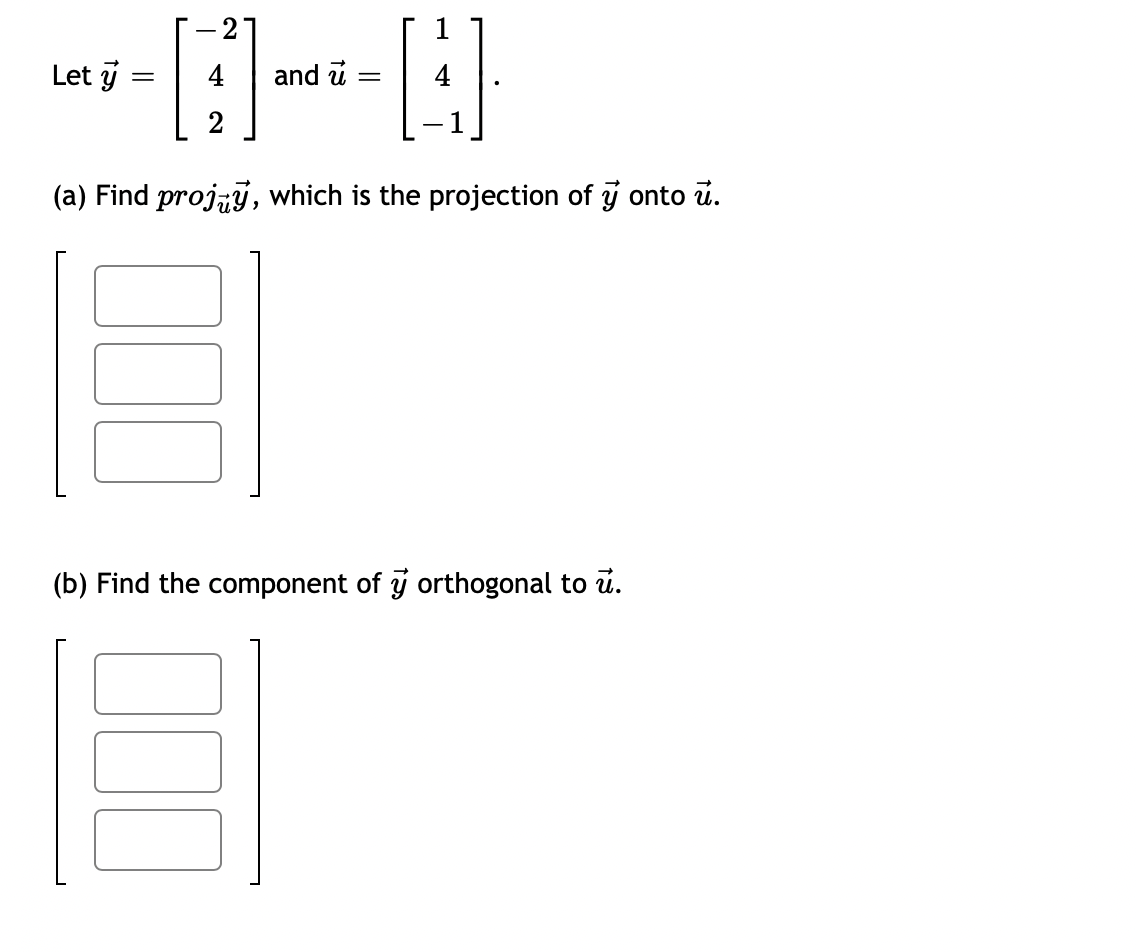
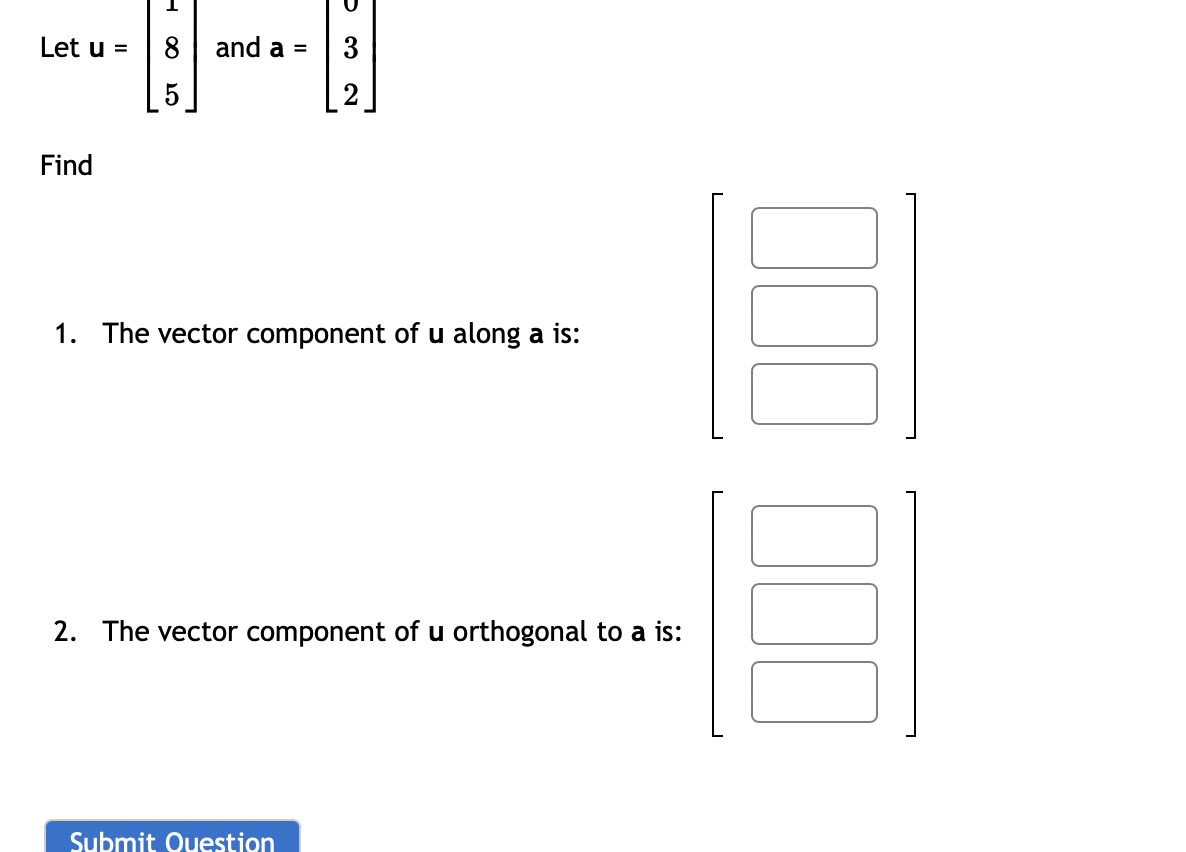
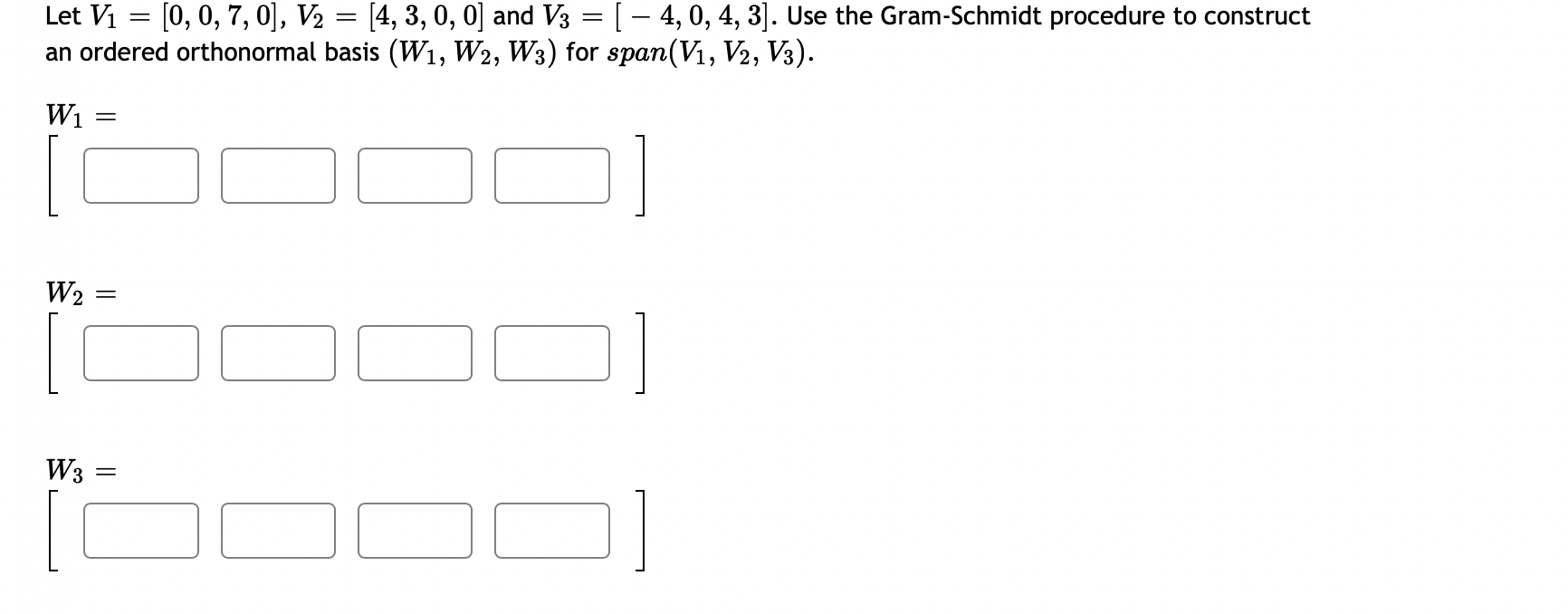
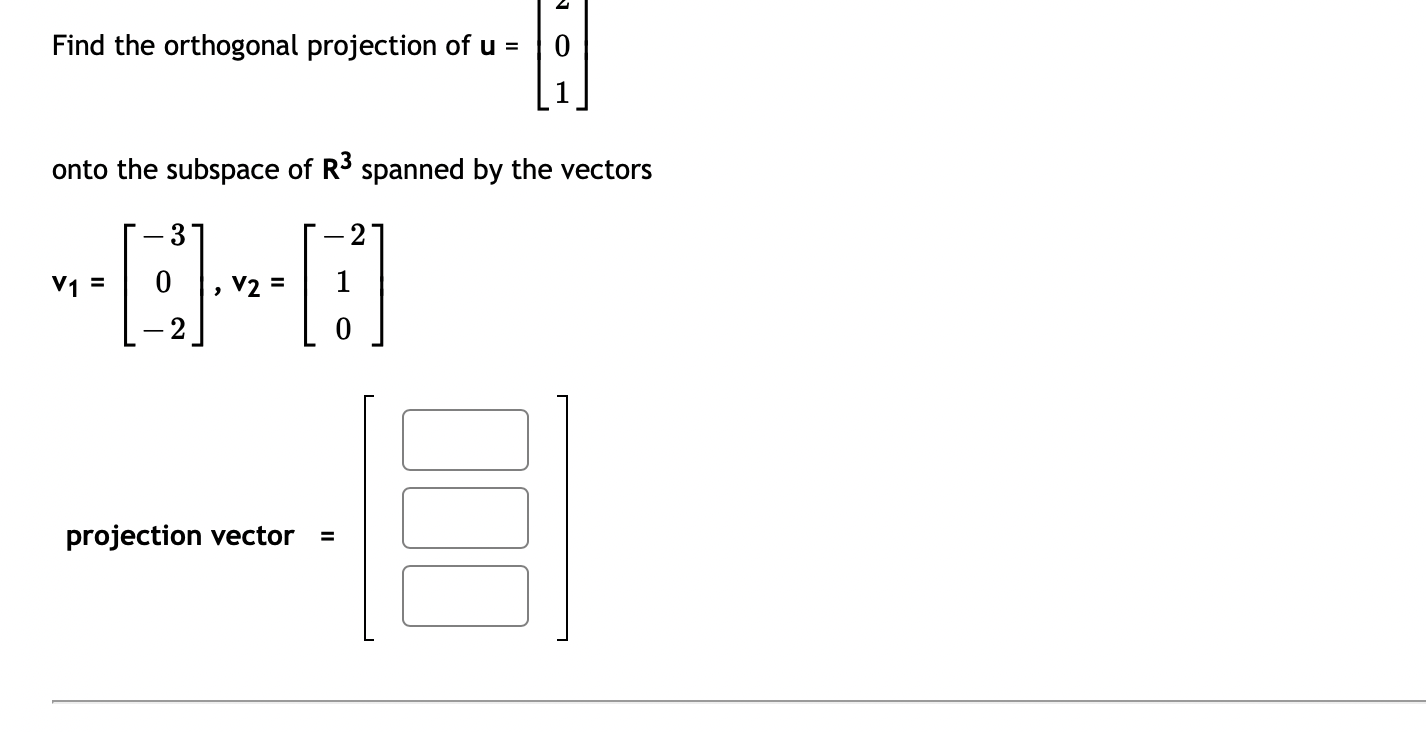
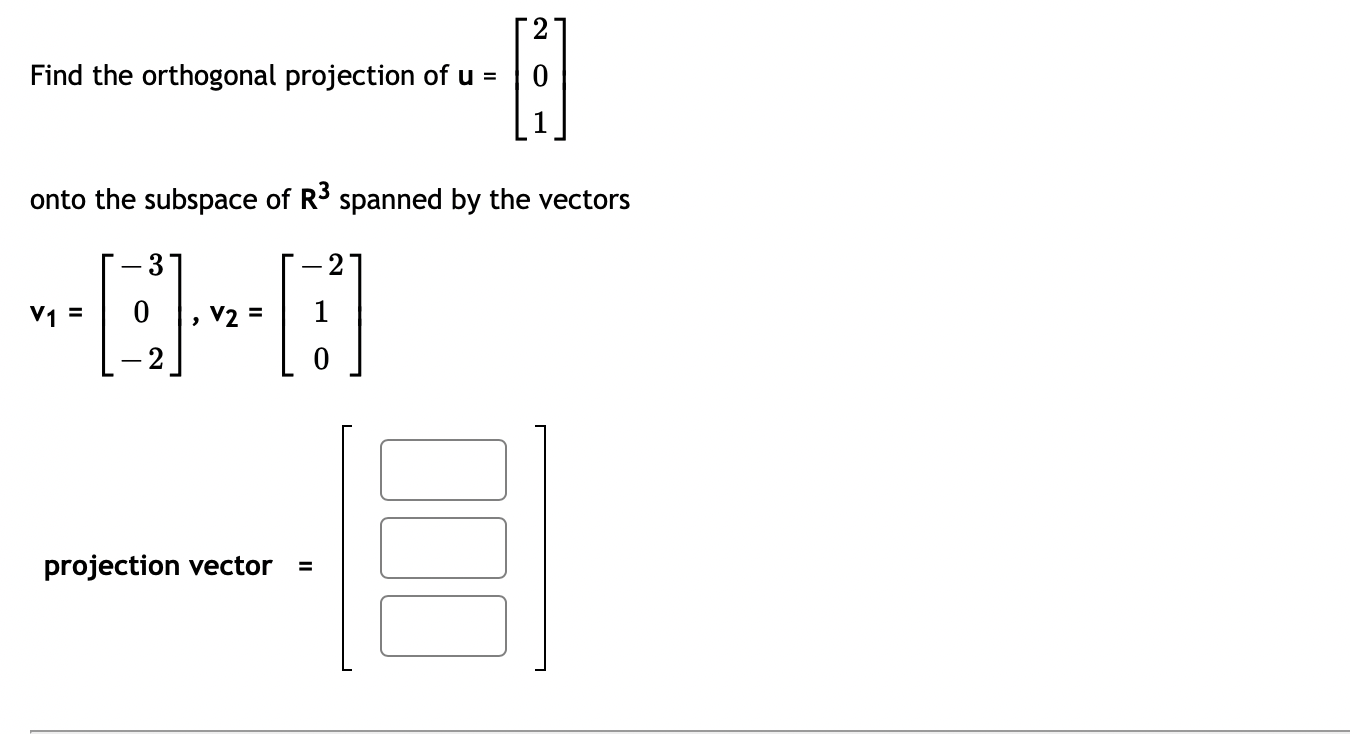
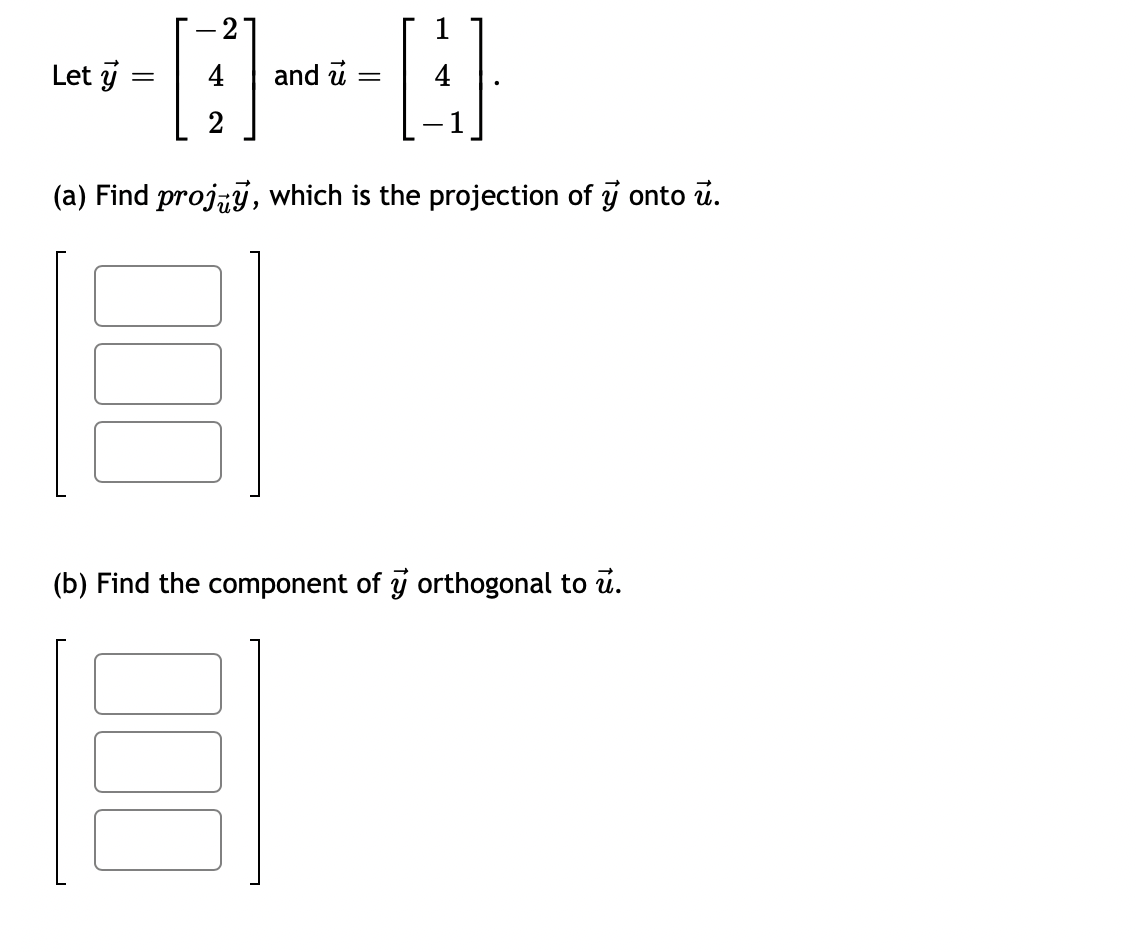
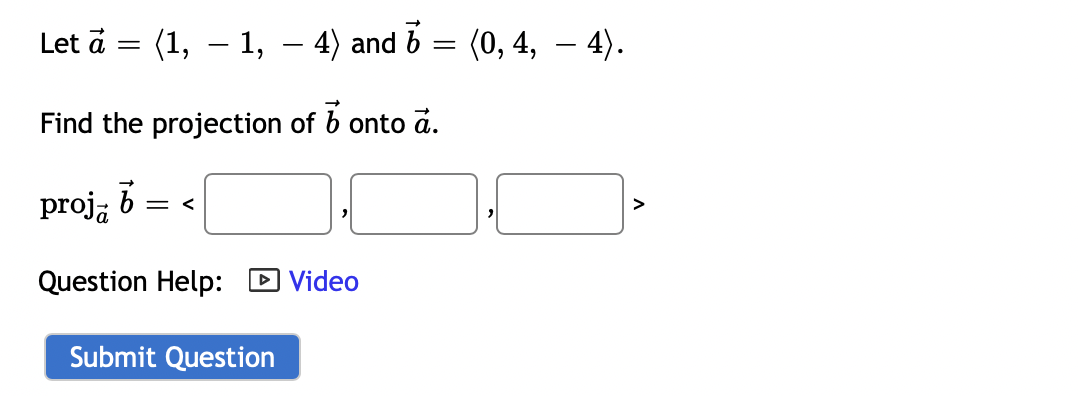
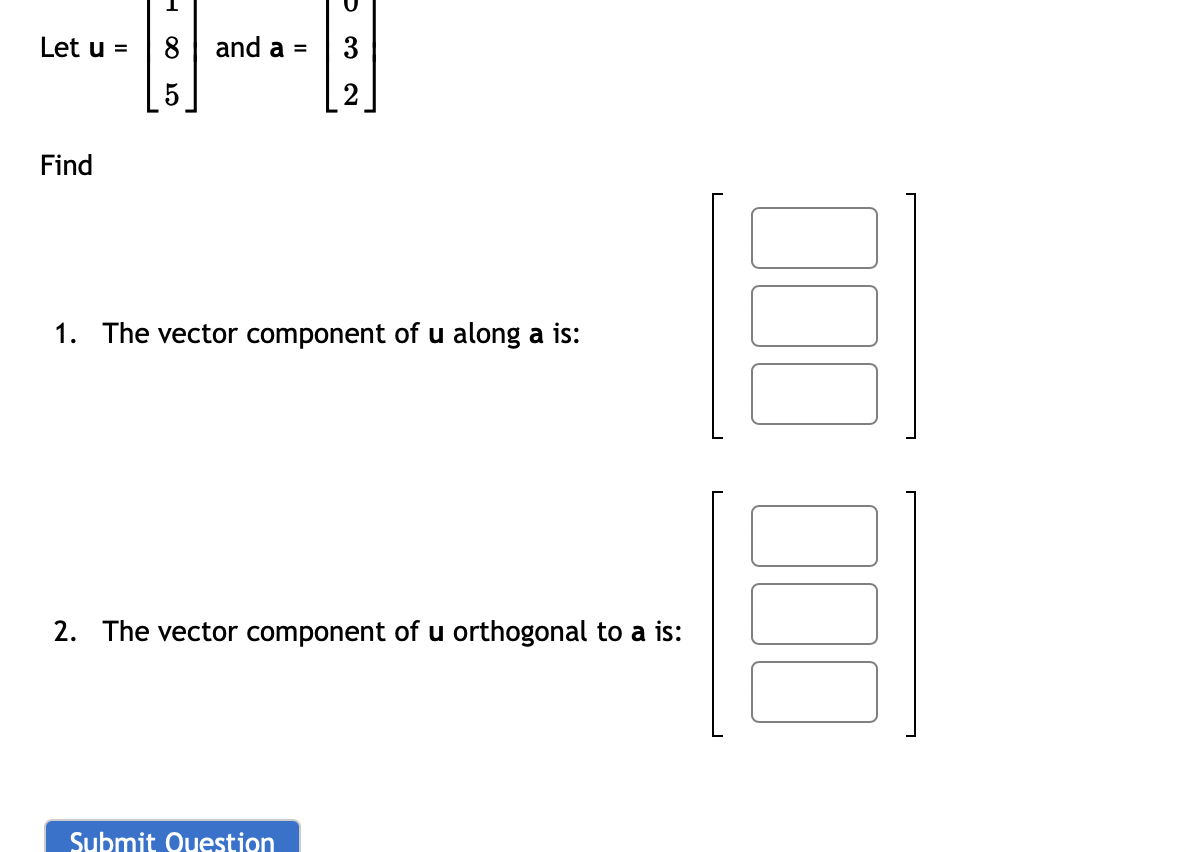
0 0 Let A = 3 3 1. Compute the eigenvalues for A (list repeated eigenvalues only once) eigenvalue 1 = ; eigenvalue 2 = 2. Find a matrix P that will diagonalize A P = 3. And compute P-1AP =3 0 1 3 The matrix A can be factored as A = PDP - _ where D = and P = 0 CO -14 If x = 3 + 8 then find Ax without computing A. 5 14 AX = Question Help: Video\fUse the weighted inner product = 1w1v1 + 2102112 for these questions. {i=[1,4]and1_3=[5, 2] Find [:1 Find ||ii|| (Give your answer in decimal form rounded to at least two places) I: Let b = ( - 3, 7, - 6) and a = (4, - 7, - 4). Compute the projection of b onto a. proja b = Compute the orthogonal projection of b onto a. orth- b = Question Help: VideoFind the orthogonal projection of u = onto the subspace of R spanned by the vectors 2 W1 = 0 V2 = O projection vector =2 Find the orthogonal projection of u = 0 1 onto the subspace of R3 spanned by the vectors 3 2 V1= 0 ,V2= 1 2 projection vector = DUB 2 1 Lets1': 4 and= 4 2 1 (a) Find proj, which is the projection of 37 onto ii. i: i: i: (b) Find the component of Q orthogonal to 17,. C] C] C] Let a = (1, - 1, - 4) and b = (0, 4, - 4). Find the projection of b onto a. proja b = Question Help: D Video Submit QuestionLet u = 8 and a = OT Find 1. The vector component of u along a is: IFI 2. The vector component of u orthogonal to a is: Submit Question1 2 4 Let S be the subspace of R3 spanned by the vectors 1 and 1 , and let 5 = 2 . Find the point in S 1 4 5 that is closest to b. (If the entries of your vector do not come out as whole numbers, round them to 4 decimal places.) [:1 C] :1 1 1 1 2 LetA: 2 1 0 and3= 1 2 1 0 4 1 0 1 0 Find the least-squares solution to A5 = 3. Enter the solution using fractions if necessary -- no decimals! {3\" = Enter the error vector below. Use fractions if necessary -- no decimals! AgeE: C] C] C] C] What is the magnitude of the error? (decimals 0k!) I Find a least-squares best fit line for the points (1, 1), (2, 4), (3,4), (4, 5). Write your answer as a function of w. P: Find the least-squares solution to the following system of equations: 2::1 9:2 = 3 2x1 2.12 = 8 3am + 4.12 = 7 [C] C] Submit
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


