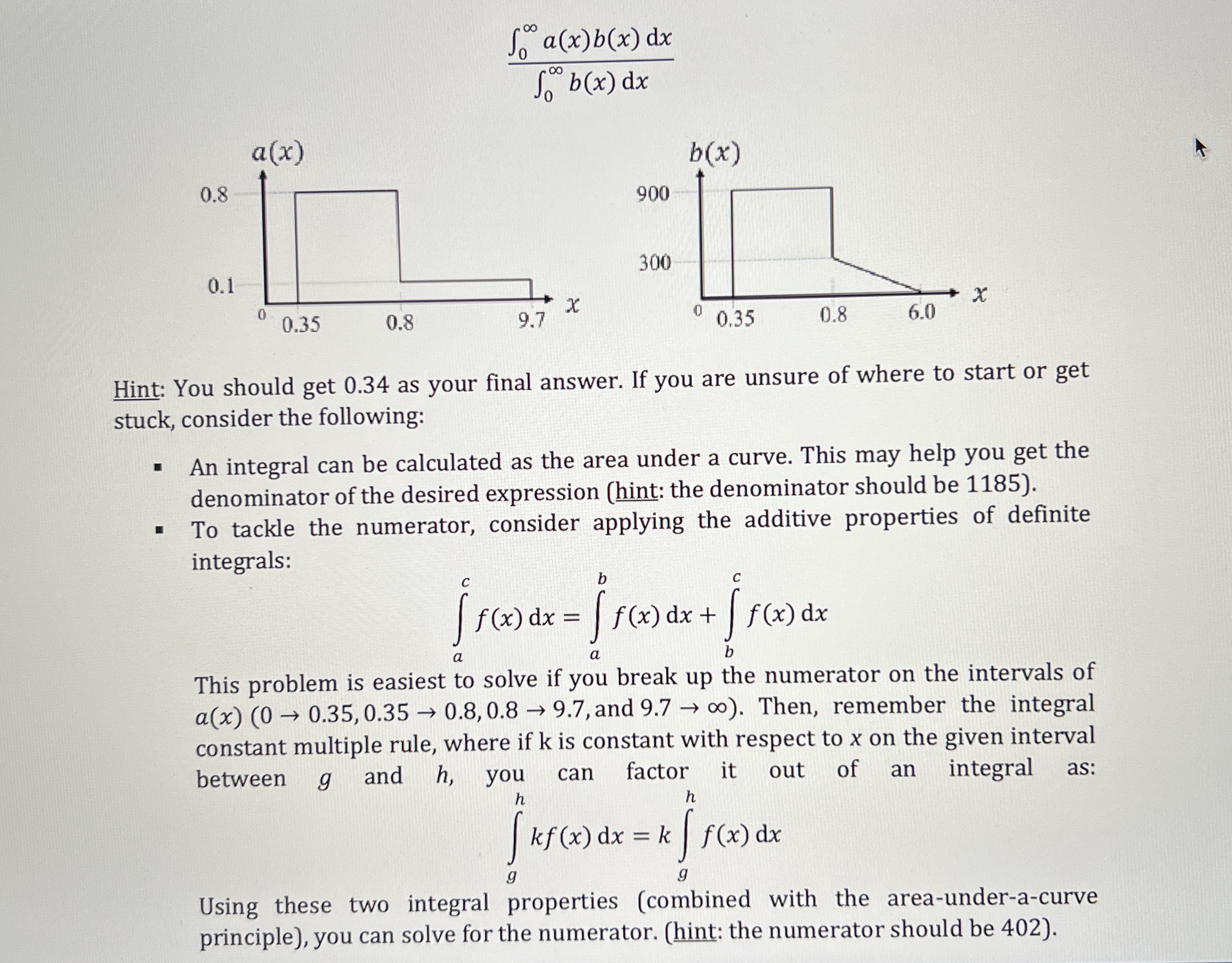
Question: 0 a ( x ) b ( x ) d x 0 b ( x ) d x Hint: You should get 0 . 3
Hint: You should get as your final answer. If you are unsure of where to start or get stuck, consider the following:
An integral can be calculated as the area under a curve. This may help you get the denominator of the desired expression hint: the denominator should be
To tackle the numerator, consider applying the additive properties of definite integrals:
This problem is easiest to solve if you break up the numerator on the intervals of and Then, remember the integral constant multiple rule, where if k is constant with respect to on the given interval between and you can factor it out of an integral as:
Using these two integral properties combined with the areaunderacurve principle you can solve for the numerator. hint: the numerator should be
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


