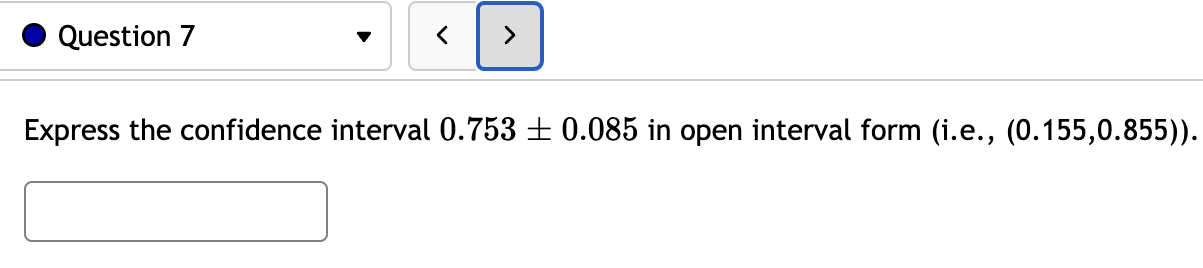
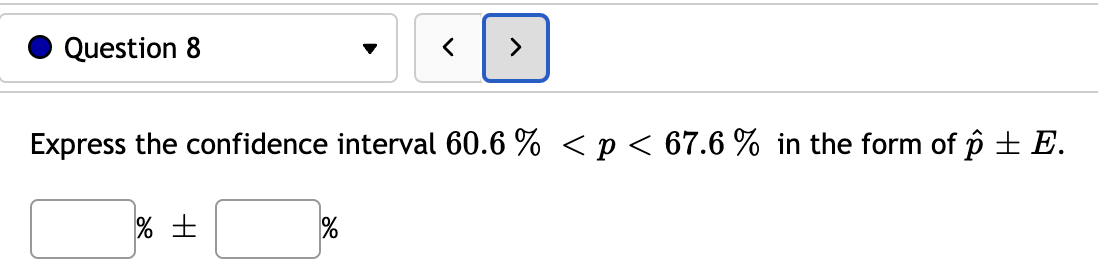
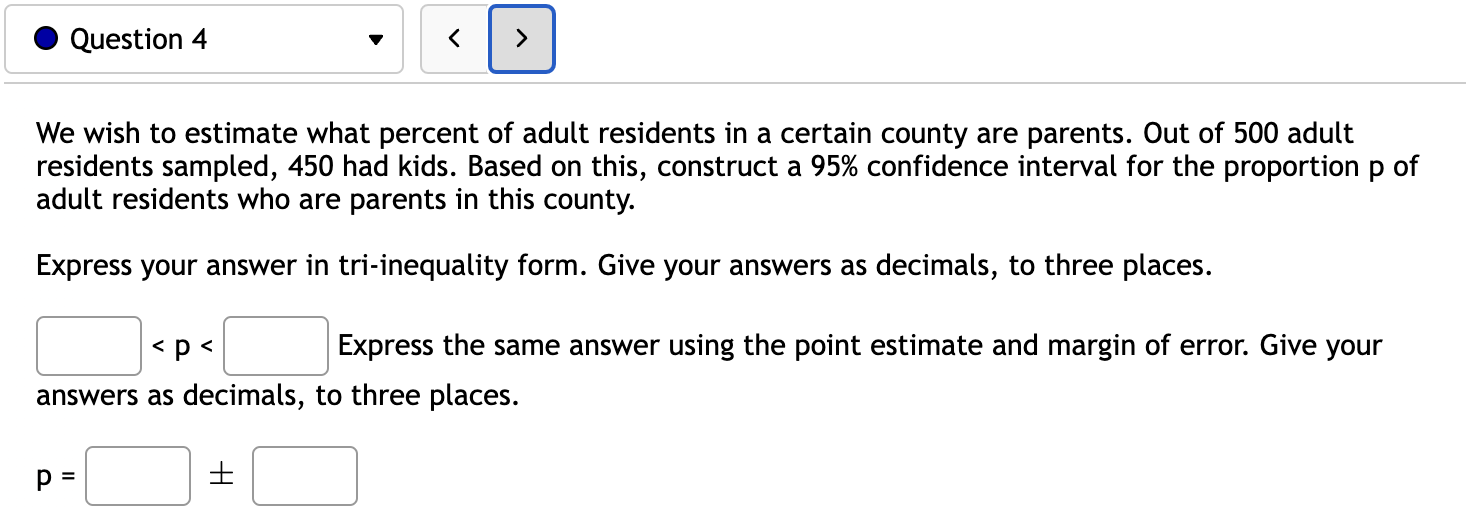
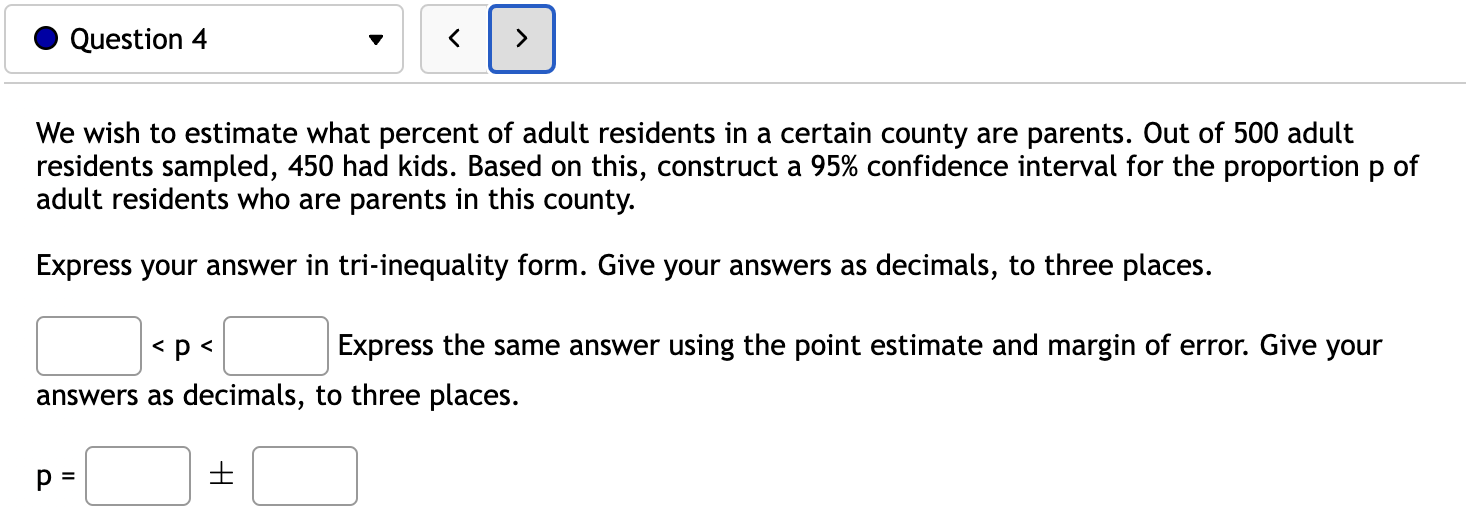
0 Question 1 v You are interested in constructing a 90% confidence interval for the proportion of all caterpillars that eventually become butterflies. 0f the 383 randomly selected caterpillars observed, 56 lived to become butterflies. Round answers to 4 decimal places where possible. a. With 90% confidence the proportion of all caterpillars that lived to become a butterfly is between C] and C]. b. If many groups of 383 randomly selected caterpillars were observed, then a different confidence interval would be produced from each group. About C] percent of these confidence intervals will contain the true population proportion of caterpillars that become butterflies and about C] percent will not contain the true population proportion. 0 Question 2 v I If n = 520 and X = 416, construct a 95% confidence interval for the population proportion, p. Give your answers to three decimals

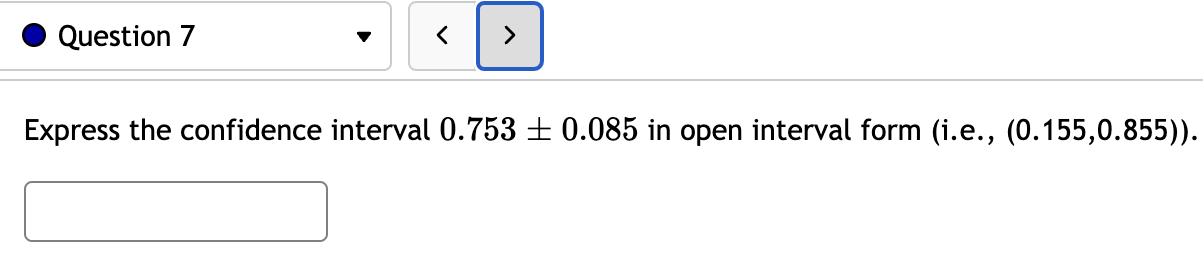
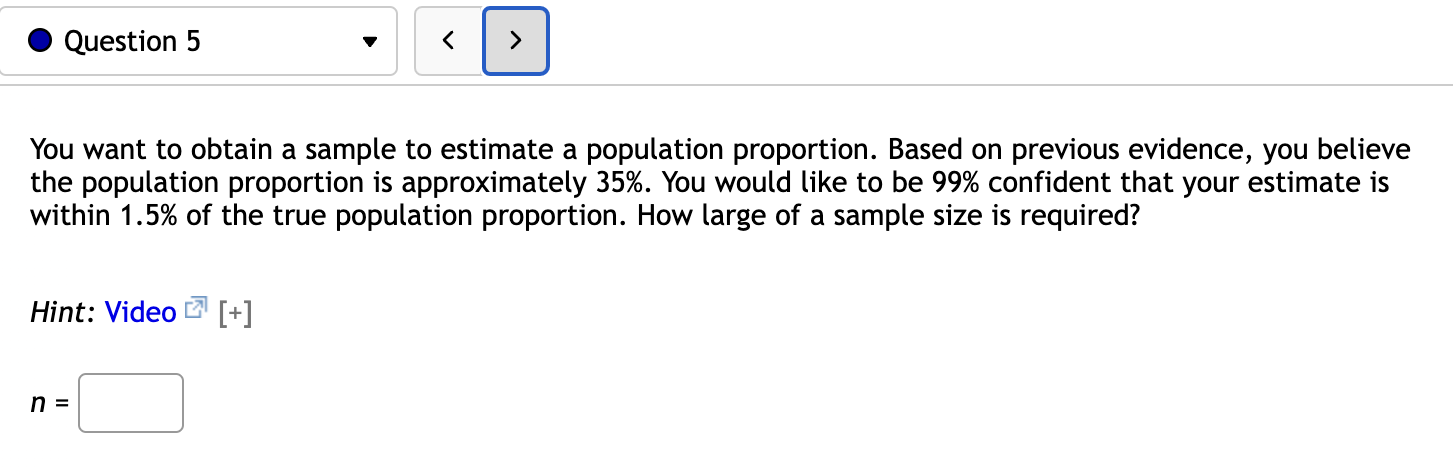
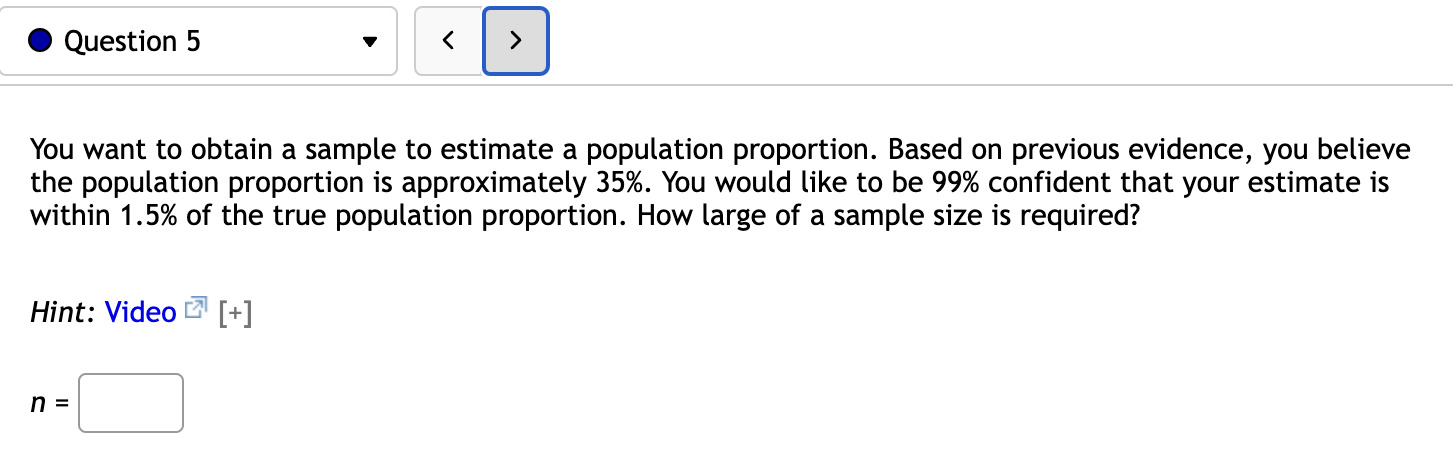
Assume that a sample is used to estimate a population proportion p. Find the margin of error M.E. that corresponds to a sample of size 102 with 14.7% successes at a confidence level of 99.5%. M.E. = % Answer should be obtained without any preliminary rounding. However, the critical value may be rounded to 3 decimal places. Round final answer to one decimal place 0 Question 1 v A political candidate has asked you to conduct a poll to determine what percentage of people support him. If the candidate only wants a 2.5% margin of error at a 97.5% confidence level, what size of sample is needed? When finding the z-value, round it to four decimal places. Hint: Video [+] 0 Question 2 v A political candidate has asked you to conduct a poll to determine what percentage of people support her. If the candidate only wants a 4% margin of error at a 99% confidence level, what size of sample is needed? Give your answer in whole people