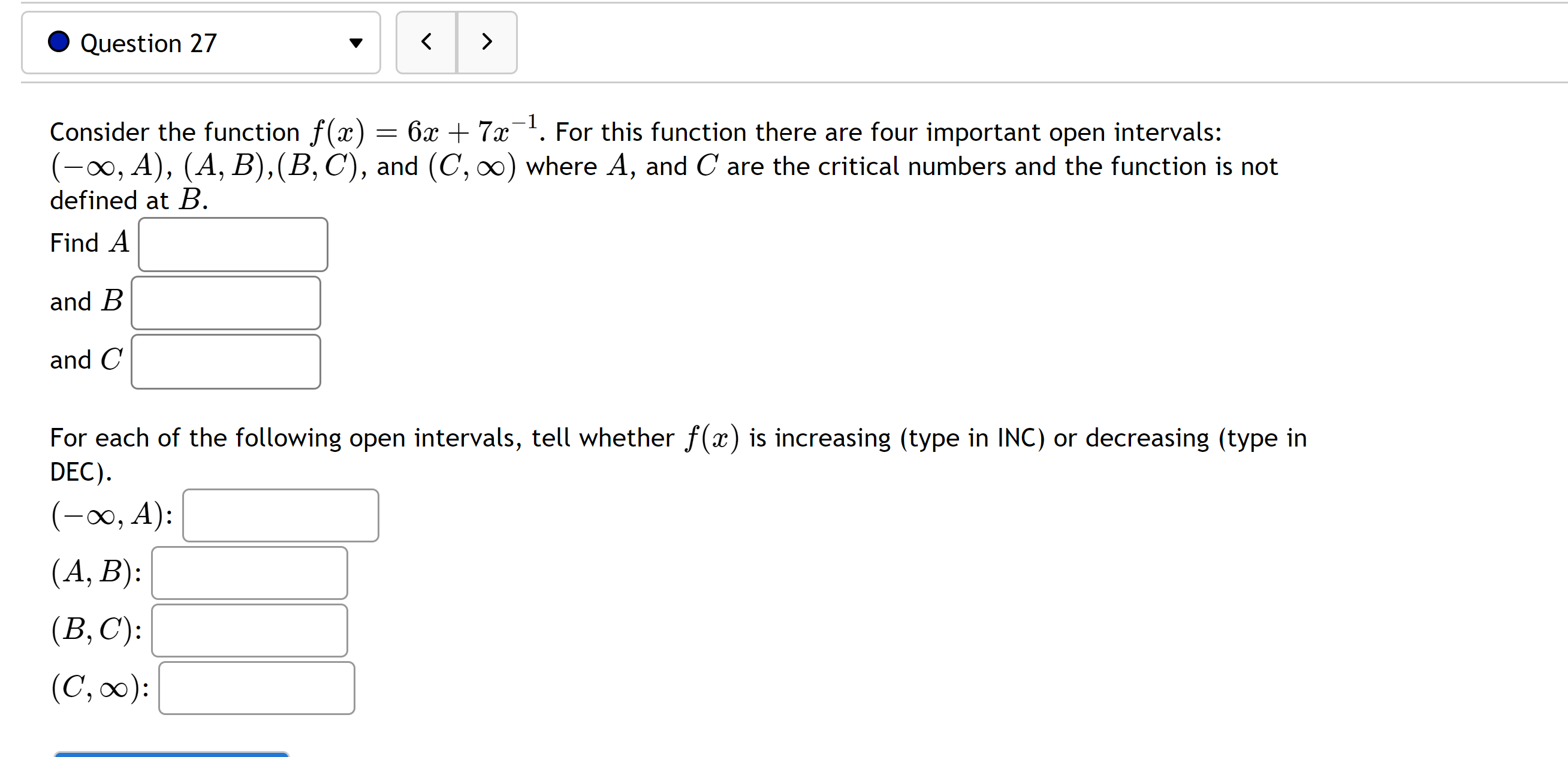
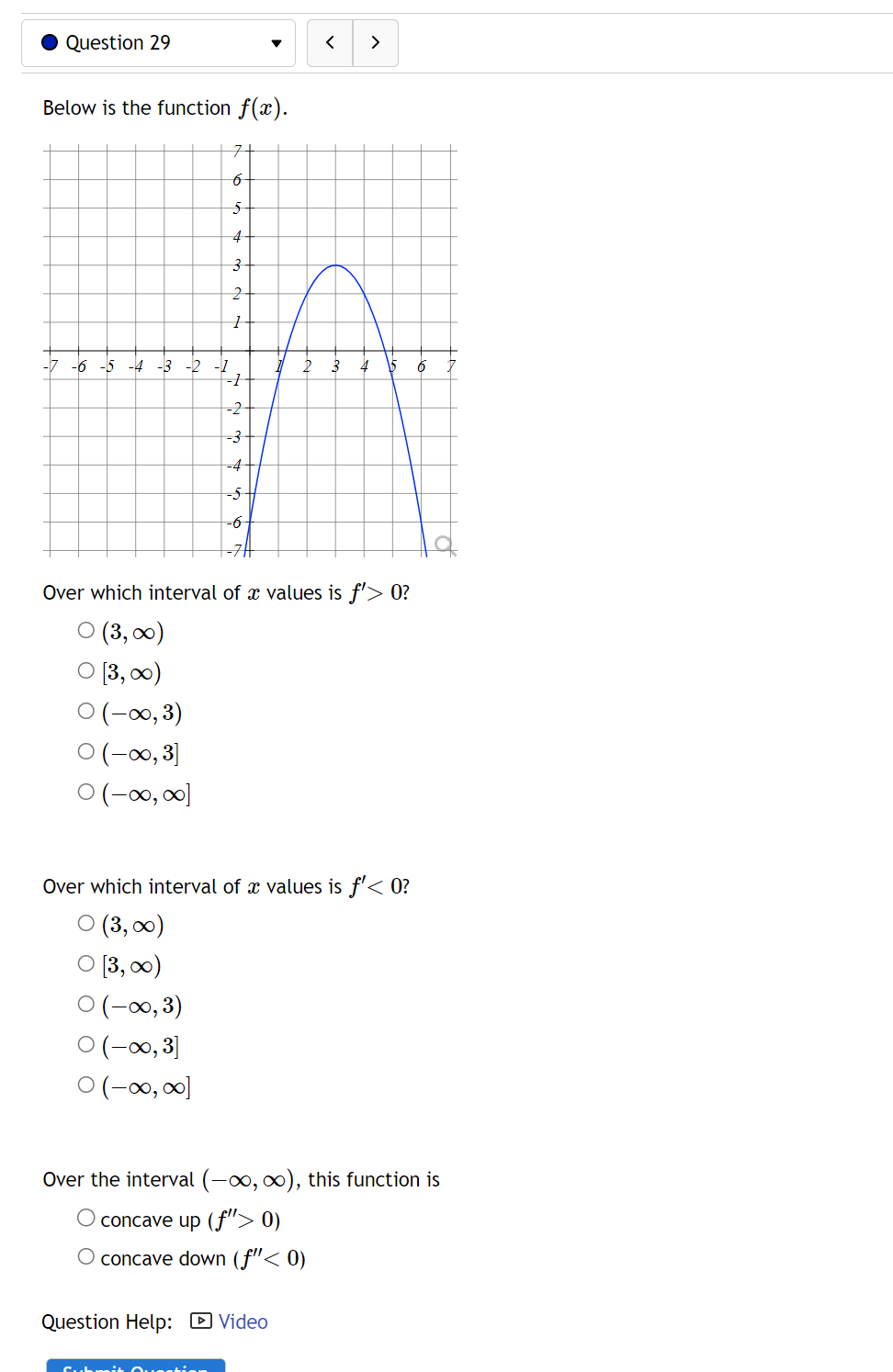
0 Question 24 v The function f(m) = 2a:3 + 1.715132 + 111.74642: + 7.74 is increasing on the open interval ( C] , E ). It is decreasing on the open interval ( 00, C] ) and the open interval ( C] , 00 ). The function has a local maximum at C] . Question 25 Consider the function f(x) = 12x + 30x - 300x3 + 7. For this function there are four important intervals: (-0o, A], [A, B], [B, C'], and [C, co) where A, B, and C are the critical numbers. Find A and B and C At each critical number A, B, and C does f(a) have a local min, a local max, or neither? Type in your answer as LMIN, LMAX, or NEITHER. At A At B At C0 Question 26 V Consider the function at) 2 2x3 + 42x2 24023 + 8. For this function there are three important open intervals: (700, A), (A, B), and (B, 00) where A and B are the critical numbers. For each of the following open intervals, tell whether f(x) is increasing (type in INC) or decreasing (type in DEC) (700714]:l l (A,B):l \\ (B, 00M \\ Question Help: E] Video Question 27 Below is the function f(w). mmwu Over Wiich interval of 1' values is f'> 0? O (3, 00) O [3, 00) 0 (700,3) 0 (7003)] 0 (700,00] Over which interval of a: values is f' 0) O concave down (f" Video