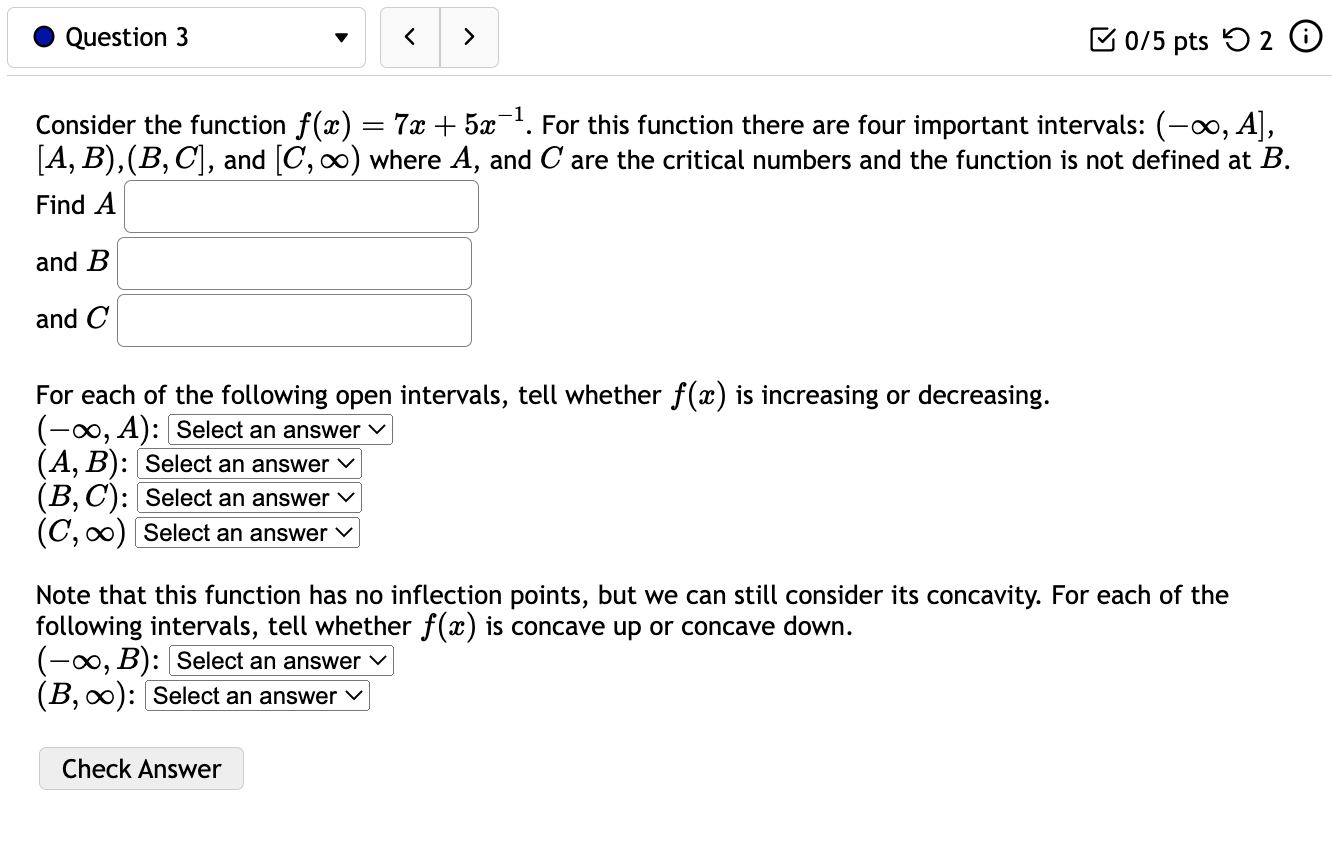
Question: 0 Question 3 V E 0/5 pts '0 2 6) Consider the function f(:c) = 73: + 5:1:'1. For this function there are four important
![four important intervals: (00, A], [A, B),(B, C], and [0, 00) where](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66615eaba4fcc_25966615eab8b86c.jpg)
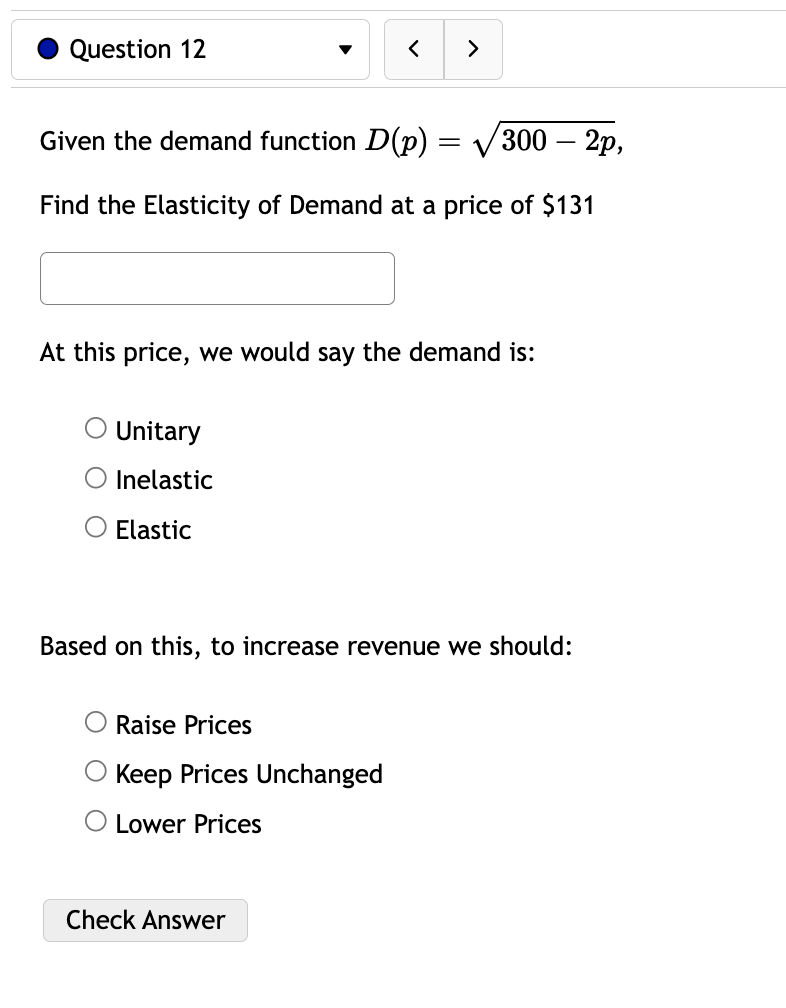
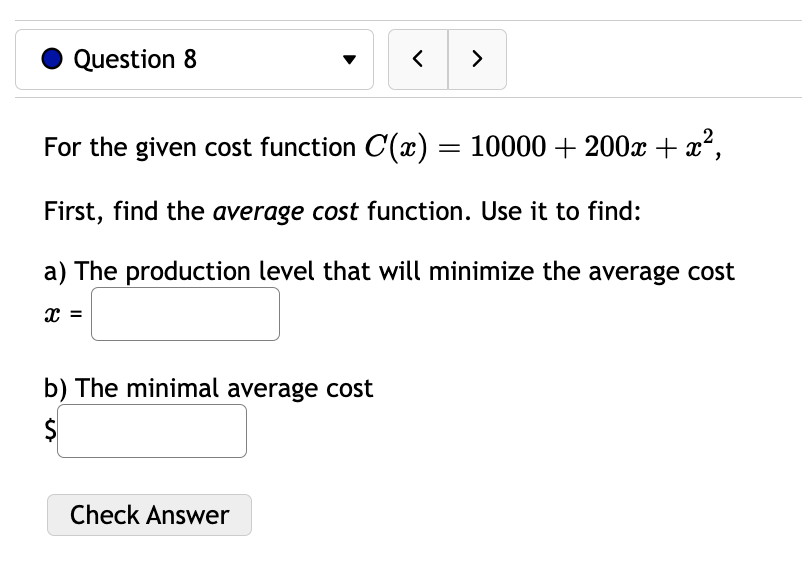
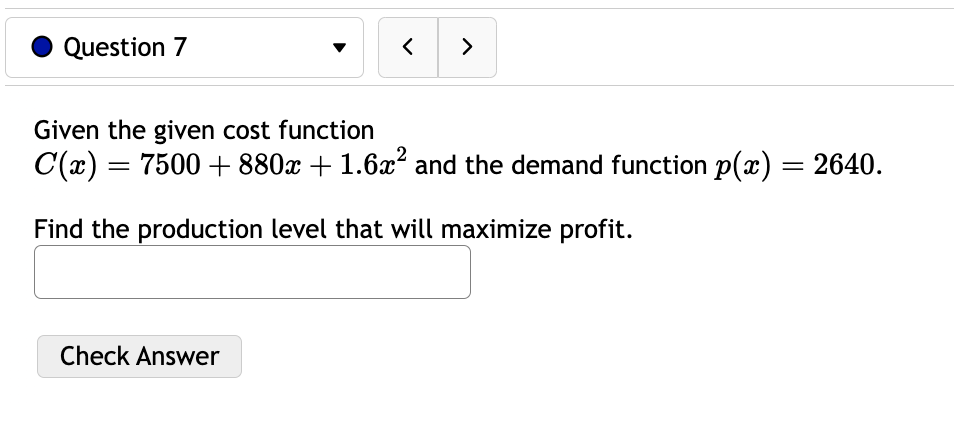
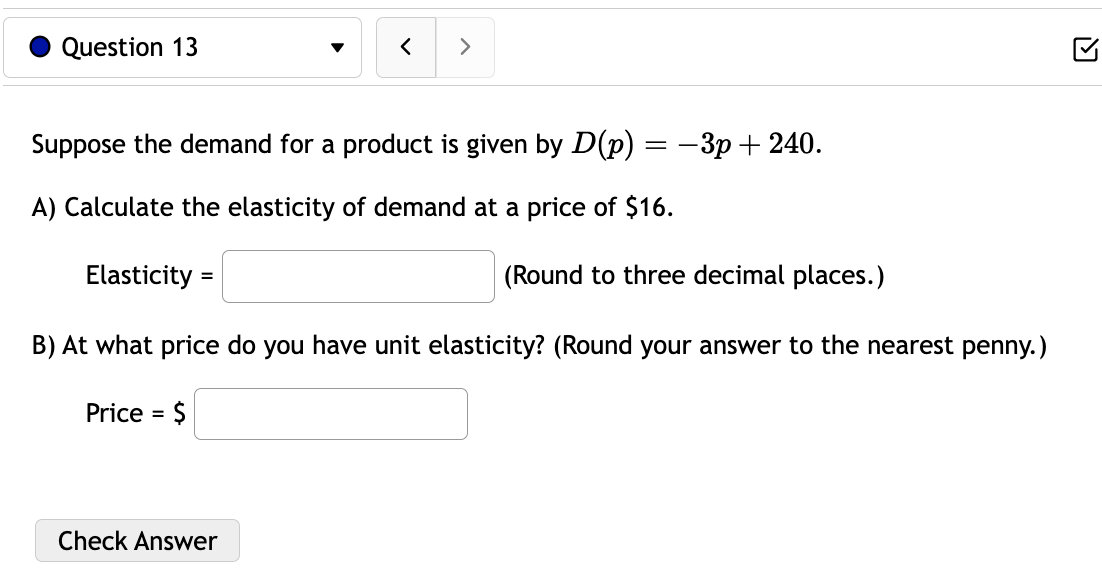
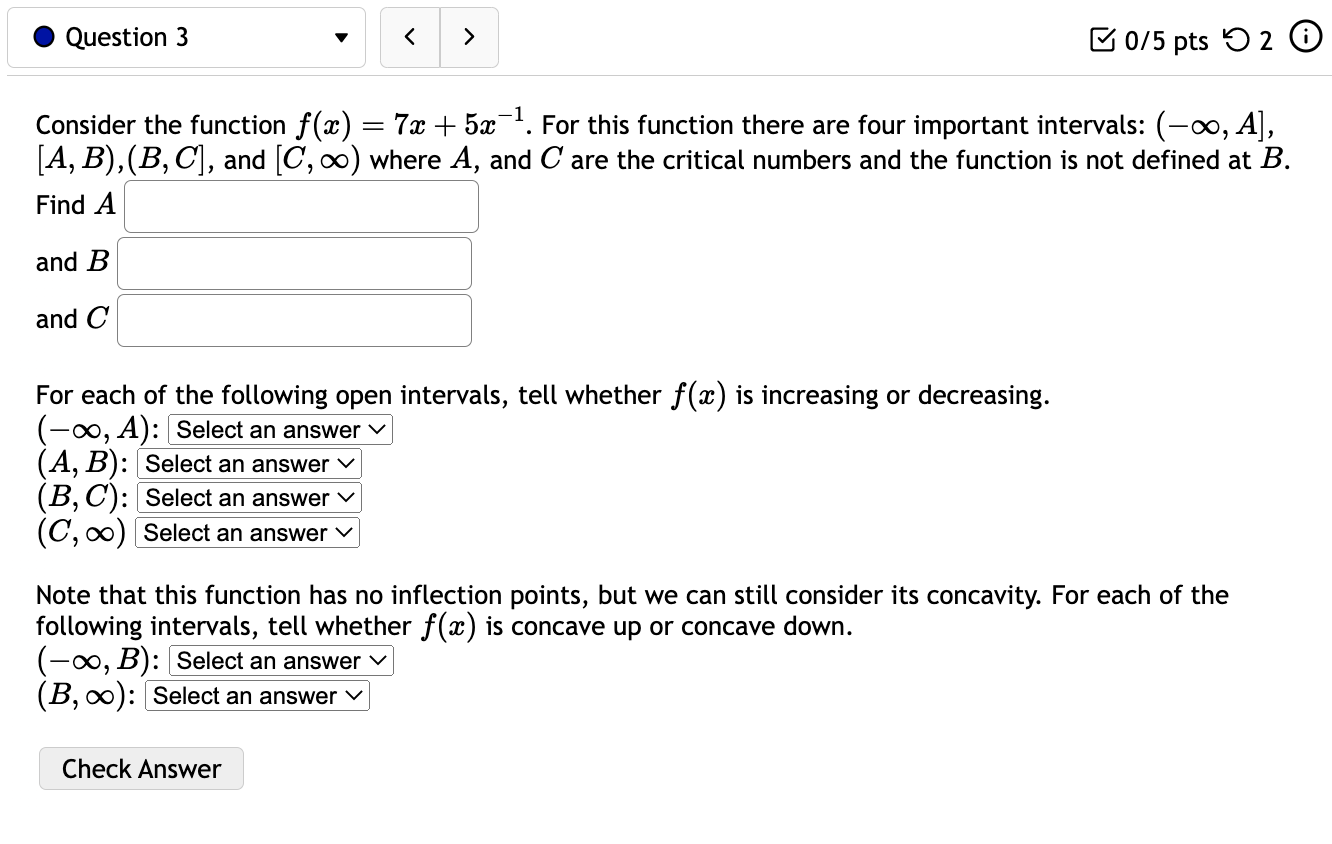
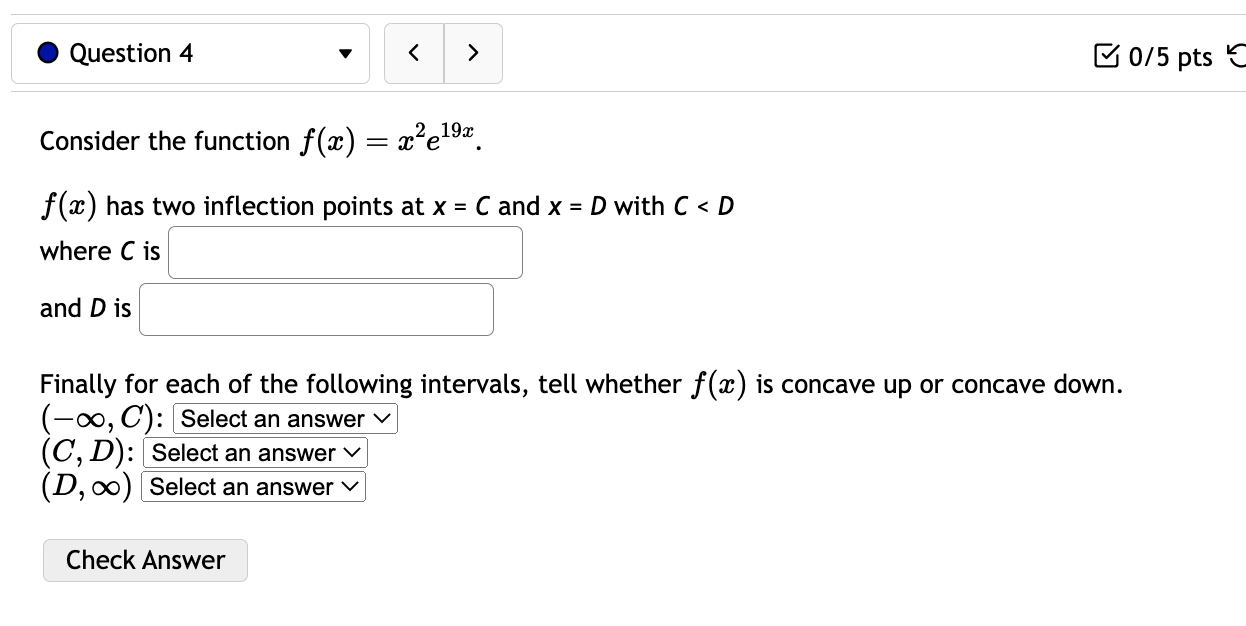
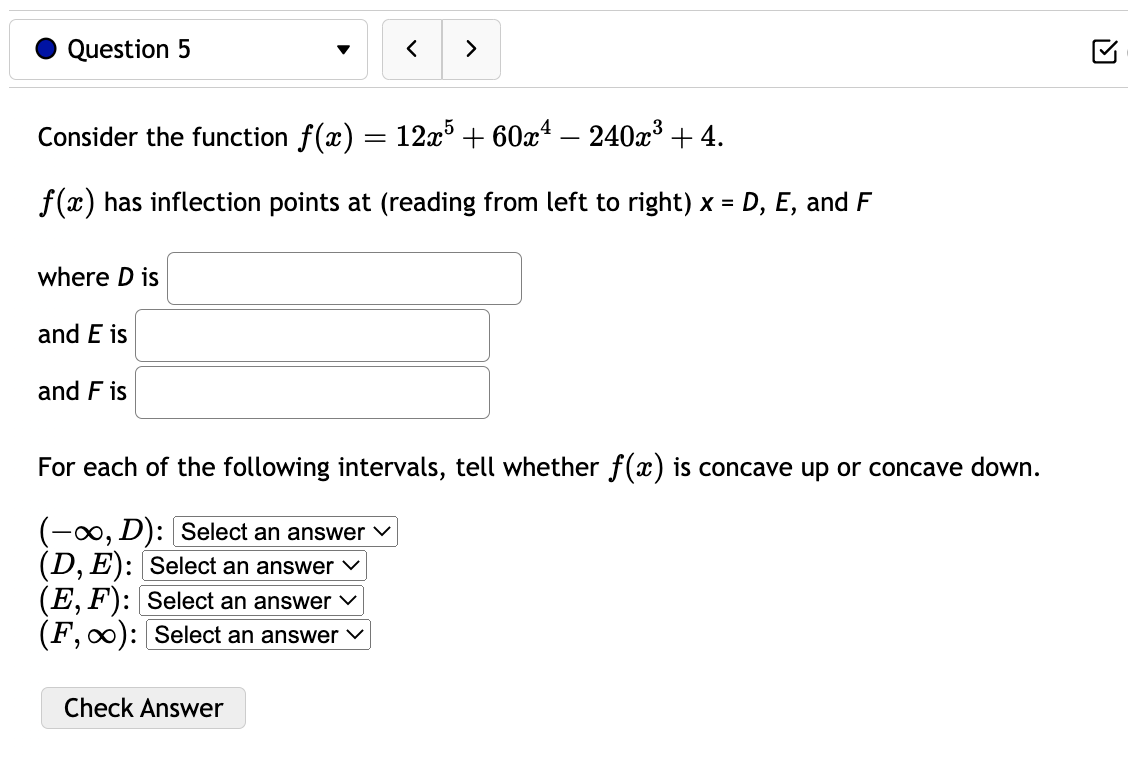
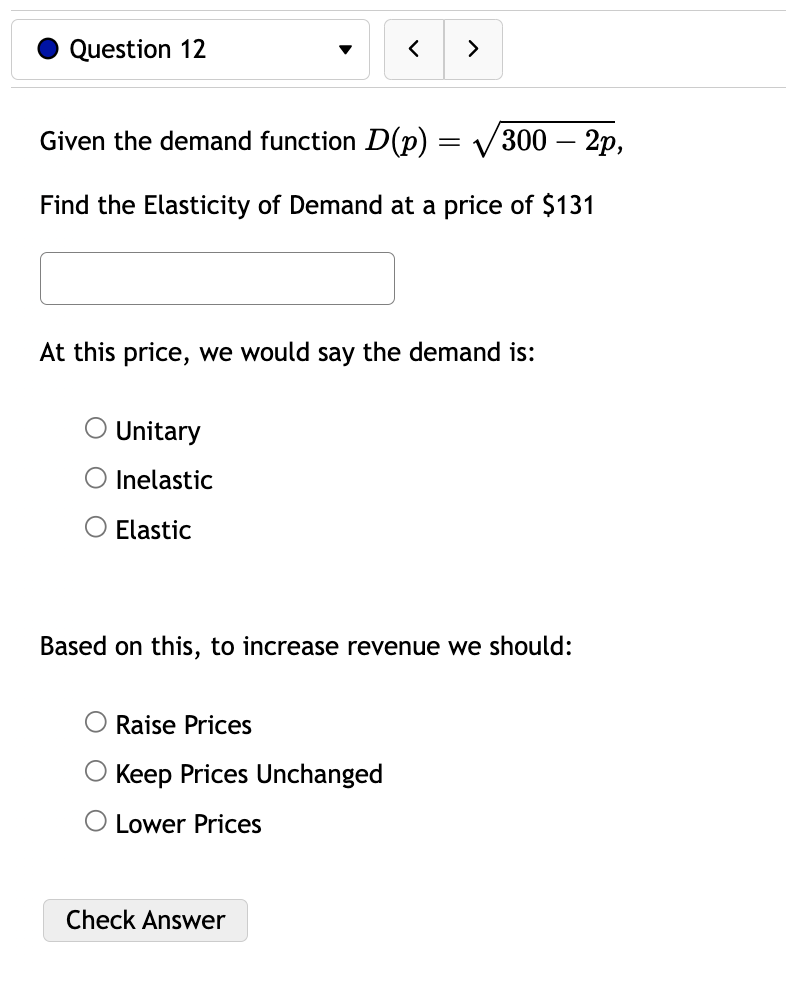
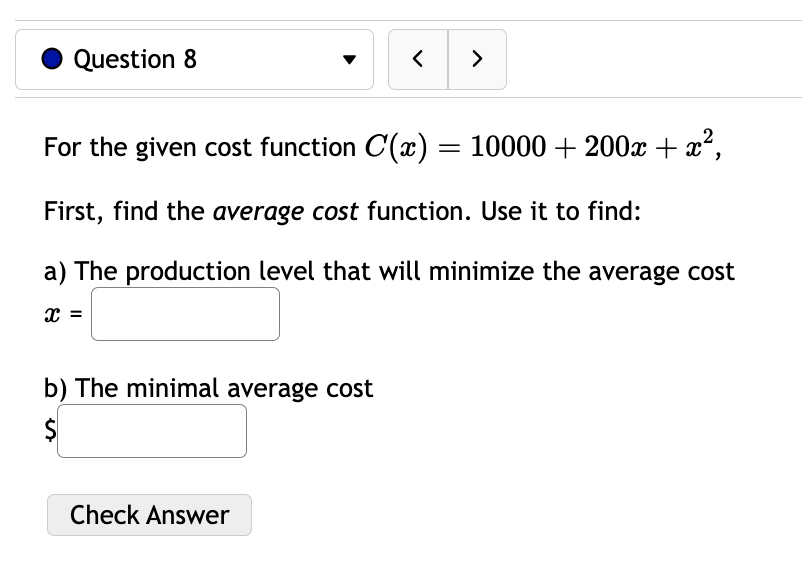
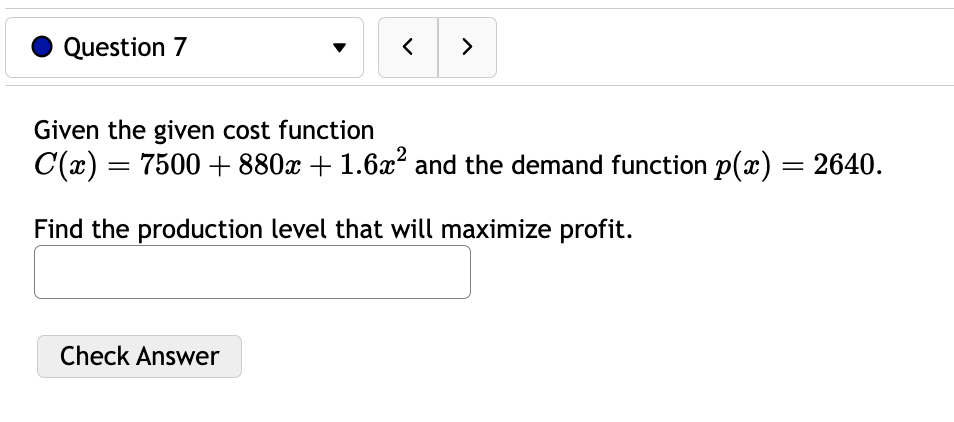
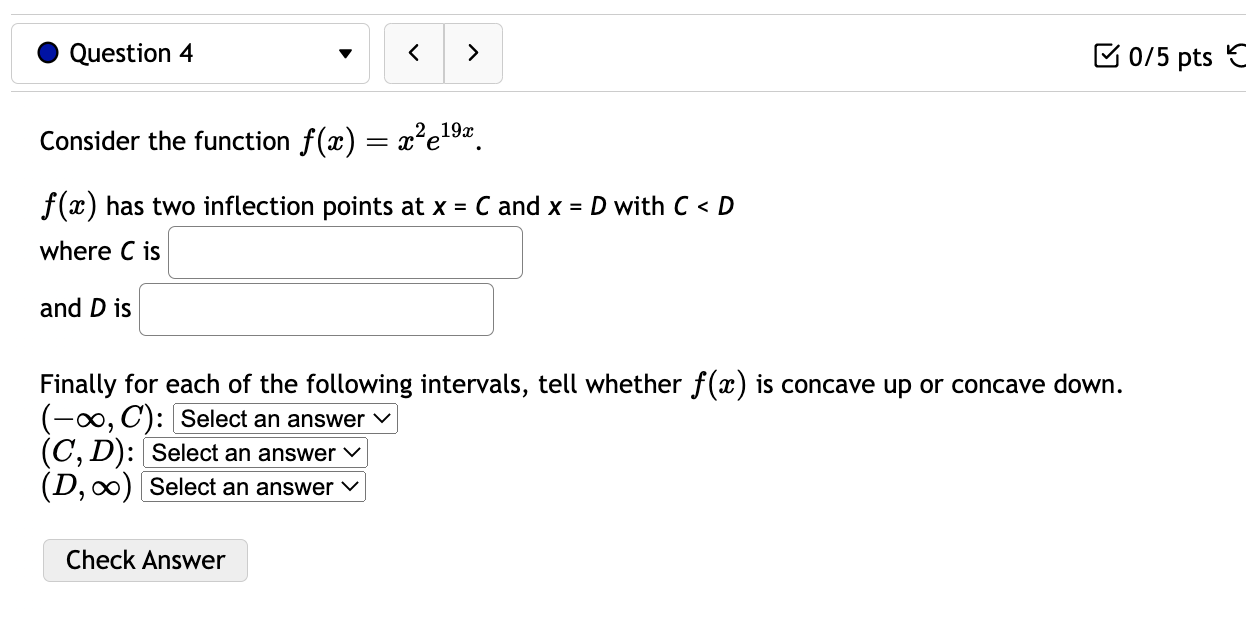
0 Question 3 V E 0/5 pts '0 2 6) Consider the function f(:c) = 73: + 5:1:'1. For this function there are four important intervals: (00, A], [A, B),(B, C], and [0, 00) where A, and C are the critical numbers and the function is not defined at B. Find A l and B ' ' and C ' ' For each of the following open intervals, tell whether zz) is increasing or decreasing. (oo,A)= (AB): (3,0): (0,00) Note that this function has no inflection points, but we can still consider its concavity. For each of the following intervals, tell whether f(:c) is concave up or concave down. (-0033): (B, 00): Check Answer 0 Question 4 v I3 015 pts '5: 2 619$. Consider the function f(a:) = a: x) has two inflection points at x = C and x = D with C Consider the function x) 2 12:35 -l 603:4 240333 + 4. f(a:) has inflection points at (reading from left to right) x = D, E, and F where D is ' ' and E is ' \ ' and F is ' ' For each of the following intervals, tell whether f(a:) is concave up or concave down. (-00:19): (13:13): (Em): (F, co): Check Answer 0 Question 12 v Given the demand function 13(1)) 2 V 300 2 , Find the Elasticity of Demand at a price of $131 At this price, we would say the demand is: O Unitary O Inelastic O Elastic Based on this, to increase revenue we should: 0 Raise Prices 0 Keep Prices Unchanged O Lower Prices Check Answer 0 Question 8 v For the given cost function 0(3) 2 10000 -l- 200$ -l- :32, First, find the average cost function. Use it to find: a) The production level that will minimize the average cost =8 =l J b) The minimal average cost Si J Check Answer 0 Question 7 v Given the given cost function C(m) = 7500 + 880:}: + 1.6:}:2 and the demand function p(a:) = 2640. Find the production level that will maximize profit. Check Answer 0 Question 13 v Suppose the demand for a product is given by 13(1)) 2 3p + 240. A) Calculate the elasticity of demand at a price of $16. Elasticity = (Round to three decimal places.) 3) At what price do you have unit elasticity? (Round your answer to the nearest penny.) Price = S Check
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


