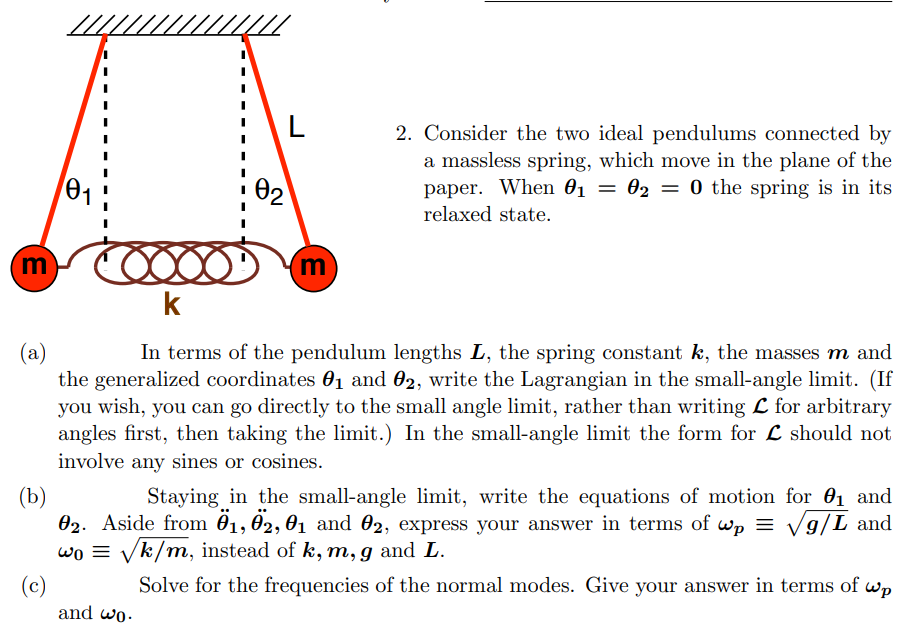
01 L m 2. Consider the two ideal pendulums connected by a massless spring, which move in the plane of the paper. When 0 = 02 = 0 the spring is in its 01 relaxed state. (a) (b) (c) k In terms of the pendulum lengths L, the spring constant k, the masses m and the generalized coordinates 01 and 02, write the Lagrangian in the small-angle limit. (If you wish, you can go directly to the small angle limit, rather than writing angles first, then taking the limit.) In the small-angle limit the form for involve any sines or cosines. for arbitrary should not Staying in the small-angle limit, write the equations of motion for 01 and 02. Aside from 01, 02, 01 and 02, express your answer in terms of wp = /g/L and wok/m, instead of k, m, g and L. and wo. Solve for the frequencies of the normal modes. Give your answer in terms of wp E