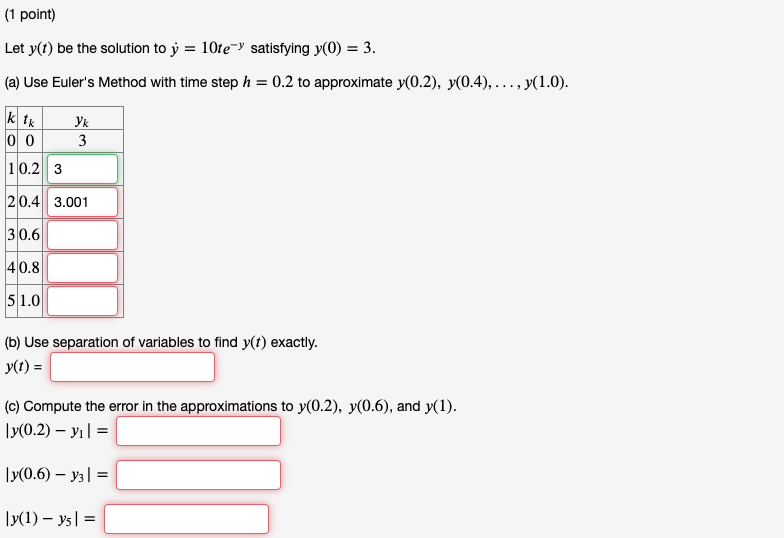
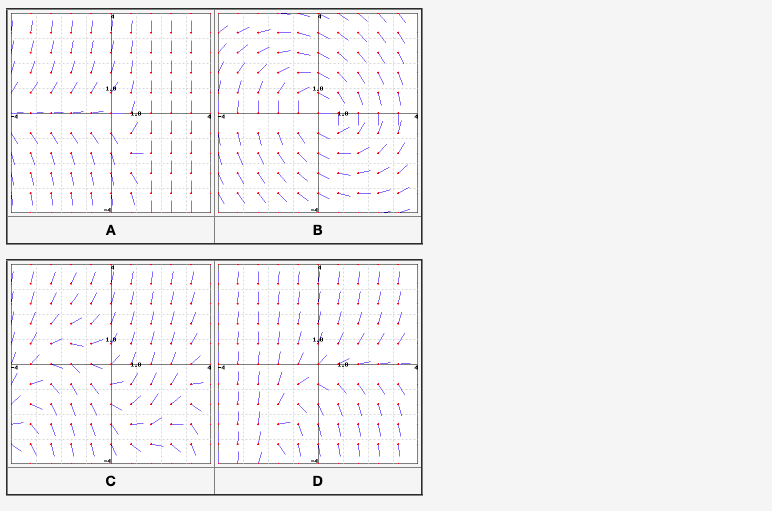
0.102 (1 point) Use linear approximation, i.e. the tangent line, to approximate as follows: Let f(x) = 1 and find the equation of the tangent line to f(x) at a "nice" point near 0.102. Then use this to approximate 0.102 0.882 (1 point) Use a linear approximation to estimate the number (8.07) 2/3 Answer: 4.0233 (1 point) Let y(t) be the solution to y = 10te satisfying y(0) = 3. (a) Use Euler's Method with time step h = 0.2 to approximate y(0.2), y(0.4), ..., y(1.0). ktk 00 3 10.2 3 20.4 3.001 30.6 40.8 51.0 (b) Use separation of variables to find y(t) exactly. y(t) = (c) Compute the error in the approximations to y(0.2), y(0.6), and y(1). |y(0.2) -y | = |y(0.6) - y3|= |y(1) - y5|= (1 point) Match the following equations with their direction field. Clicking on each picture will give you an enlarged view. While you can probably solve this problem by guessing, it is useful to try to predict characteristics of the direction field and then match them to the picture. Here are some handy characteristics to start with -- you will develop more as you practice. A. Set y equal to zero and look at how the derivative behaves along the x-axis. B. Do the same for the y-axis by setting x equal to 0 C. Consider the curve in the plane defined by setting y = 0 -- this should correspond to the points in the picture where the slope is zero. D. Setting y equal to a constant other than zero gives the curve of points where the slope is that constant. These are called isoclines, and can be used to construct the direction field picture by hand. 1. y =- = (2x + y) (2y) 2. 2 sin(x) + 1+ y 3. y = ex + 2y 4. y = 2y + xex 11 1 1 // // A B D 7