$10\mathrm{.}3-7.*$ A company will soon be introducing a new product into

a very competitive market and is currently planning its marketing

strategy. The decision has been made to introduce the product in

three phases. Phase $1$ will feature making a special introductory of$-$

fer of the product to the public at a greatly reduced price to attract

first$-$time buyers. Phase $2$ will involve an intensive advertising cam$-$

paign to persuade these first$-$time buyers to continue purchasing the

product at a regular price. It is known that another company will

be introducing a new competitive product at about the time that

phase $2$ will end. Therefore, phase $3$ will involve a follow$-$up ad$-$

vertising and promotion campaign to try to keep the regular pur$-$

chasers from switching to the competitive product.

A total of $$4$ million has been budgeted for this marketing

campaign. The problem now is to determine how to allocate this

money most effectively to the three phases. Let $m$ denote the initial

share of the market $($expressed as a percentage$)$ attained in phase $1,$

$f_2$ the fraction of this market share that is retained in phase $2,$ and

$f_3$ the fraction of the remaining market share that is retained in

phase $3.$ Use dynamic programming to determine how to allocate

the $$4$ million to maximize the final share of the market for the new

product, i$.$e$.,$ to maximize $m{f}_2{f}_3.$

$($a$)$ Assume that the money must be spent in integer multiples of

$$1$ million in each phase, where the minimum permissible mul$-$

tiple is $1$ for phase $1$ and $0$ for phases $2$ and $3.$ The following

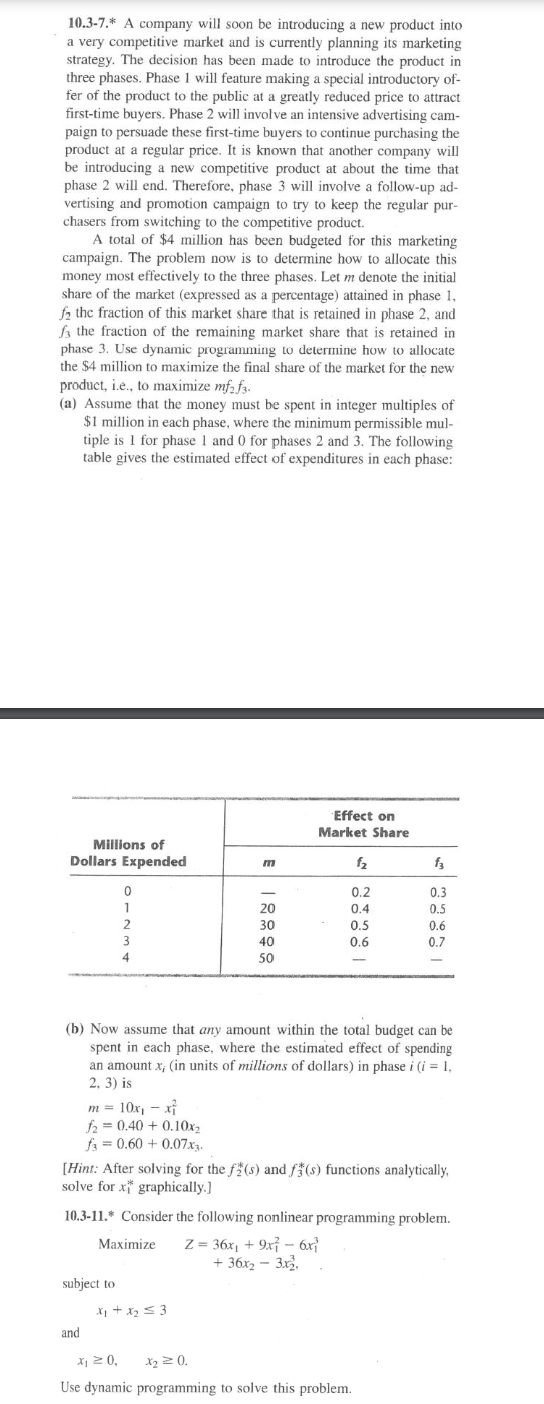
table gives the estimated effect of expenditures in each phase:

$($b$)$ Now assume that any amount within the total budget can be

spent in each phase, where the estimated effect of spending

an amount $x_i($in units of millions of dollars$)$ in phase $,$

is

$m=10x_1-x_1^2$

$f_2=0\mathrm{.}40+0\mathrm{.}10x_2$

$f_3=0\mathrm{.}60+0\mathrm{.}07x_3.$

$[$Hint: After solving for the $f_2^{**}(s)$ and $f_3^{**}(s)$ functions analytically,

solve for $x_1^{**}$ graphically.$]$

$10\mathrm{.}3-11.*$ Consider the following nonlinear programming problem.

Maximize $\{\begin{array}{c}\text{:}[Z=36x_1+9x_1^2-6x_1^3]\\ +36x_2-3x_2^3,\end{array}$

subject to

$x_1+x_{2}3$

and

$x_{1}0,x_{2}0.$

Use dynamic programming to solve this problem.