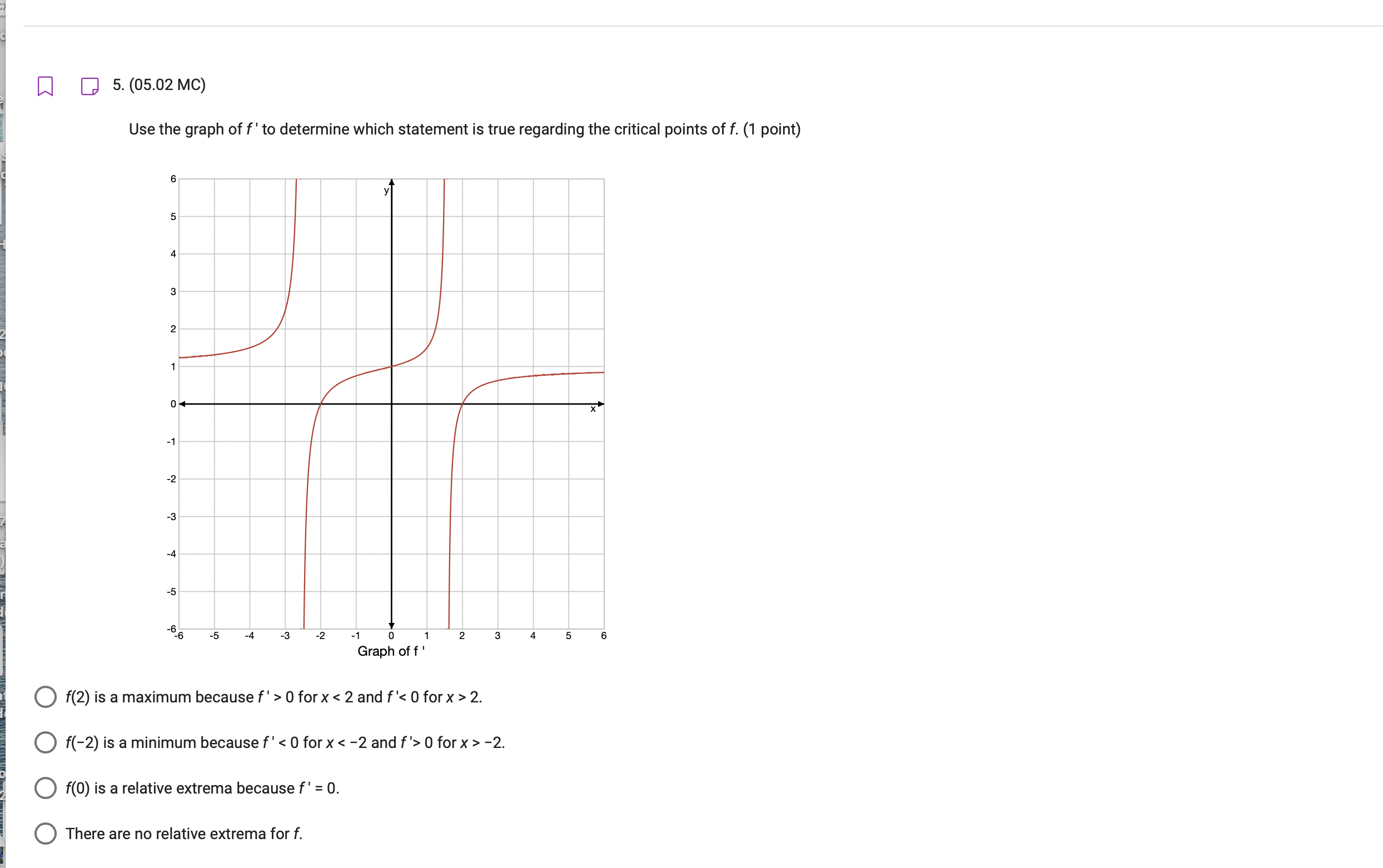
1. (05.02 MC) Given f'(x) = -2x2 determine where f(x) is decreasing. (1 point) V4 -X2 O ( -0 , - V2 ) and (V2, 0. ) O [-2, - V2) and (2, 2] O ( - 2, 2 ) O (-V2, 2] W Q 2. (05.02 MC) The table of values for f'(x) describes the behavior of continuous function f. Which of the following is true? (1 point) x 0 1 2 3 4 f'( x) -1 0 205 Of is increasing on (1, 3) only because f'(x) > 0. Of is increasing on (1, 3) and (3, 4) because f'(x) > 0. Of is decreasing on (1, 3) and (3, 4) because f'(x) > 0. Of is decreasing on (1, 3) only because f'(x) > 0.W Q 3. (05.02 MC) Given f'(x) = X2 -8x (x-4)2 , determine the x-value where a relative maximum exists for f(x). (1 point) X = 8 O X = 4 x =2 O X = 0 4. (05.02 MC) Justify why the function with f' = 2cosx + 2cosxsinx is decreasing from - to S to SH (1 point) 2 Of' ( x ) > 0 for ( # , 3. ) Of ( x ) 0 for x Of' (x) > 0 for x = 3n 25. (05.02 MC) Use the graph of f' to determine which statement is true regarding the critical points of f. (1 point) 6 A N -1 -2 -3 -4 .5 .66 -5 -3 -2 2 3 5 6 Graph of f ' Of(2) is a maximum because f' > 0 for x 2. Of(-2) is a minimum because f' 0 for x > -2. Of(0) is a relative extrema because f' = 0. O There are no relative extrema for f