Question: 1 1 Given an integer n 1, define J(n)=1+++ We want to extend the function J to other values than positive integers. The starting
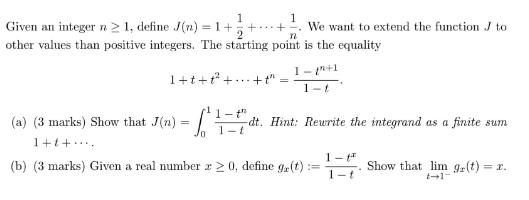
![Given any x 20, part (b) shows that ga(t) extends to a continuous function of t on [0, 1], so that the](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2023/05/64548926726d2_1683261727024.jpg)
1 1 Given an integer n 1, define J(n)=1+++ We want to extend the function J to other values than positive integers. The starting point is the equality n 1+t++ +t" = 1-th 1-t 1-1+1 1- -dt. Hint: Rewrite the integrand as a finite sum (a) (3 marks) Show that J(n) = 1+1+... (b) (3 marks) Given a real number 20, define gr(t) = 1-tt 1-t Show that lim gr(t) = =x. Given any x 0, part (b) shows that gr(t) extends to a continuous function of t on [0, 1], so that the function J(x) == L 1 - tx 1-t is defined on [0, ) and, by part (a), coincides with J(n) on positive integers. (c) (3 marks) Given any x < 0, show that lim 9x (t) asymptote at t = 0. t0+ -dt = - so that gx (t) has a vertical (d) (5 marks) Show that for x 0, we have the recurrence relation J(x+1) - J(x) = = 1 x+1 (e) (6 marks) The recurrence relation enables us to extend the definition of J(x) to all real numbers except negative integers. Compute J(1/2), J(0), and J(-1/2).
Step by Step Solution
3.51 Rating (148 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


