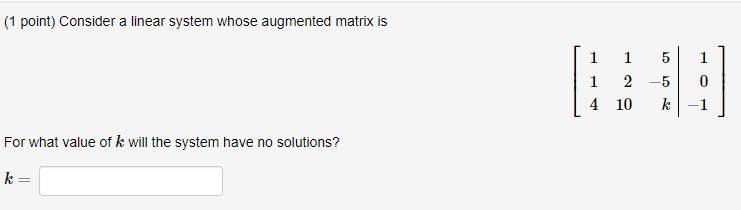
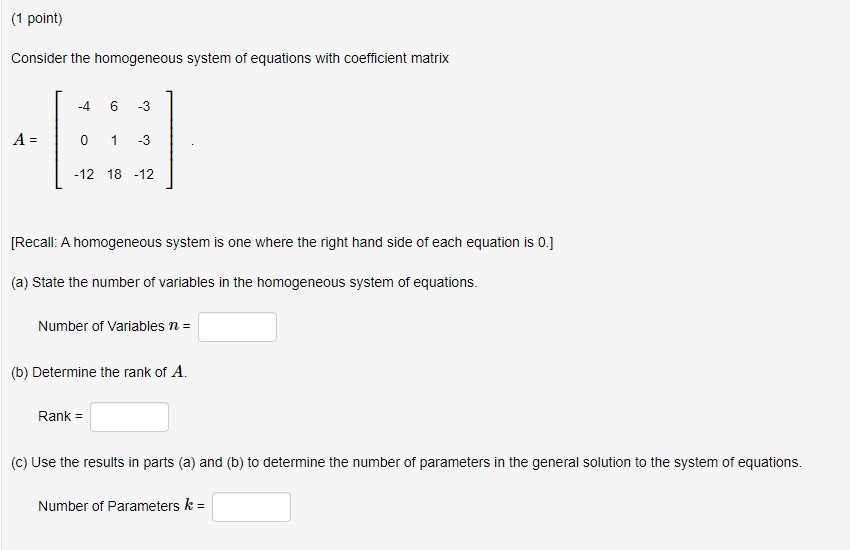
Question: 1) (1 point) FOR EACH PROBLEM ON THIS ASSIGNMENT, ENSURE THAT YOU TAKE NOTE OF HOW MANY ATTEMPTS ARE GIVEN. SOME OF THE PROBLEMS MAY
1)
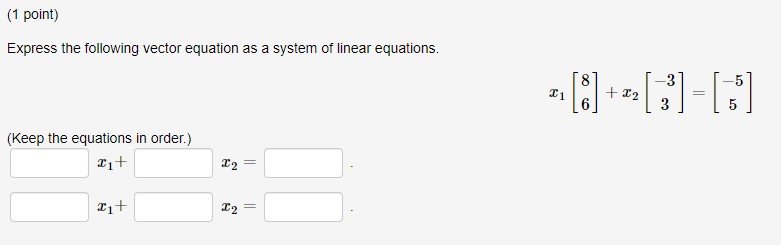
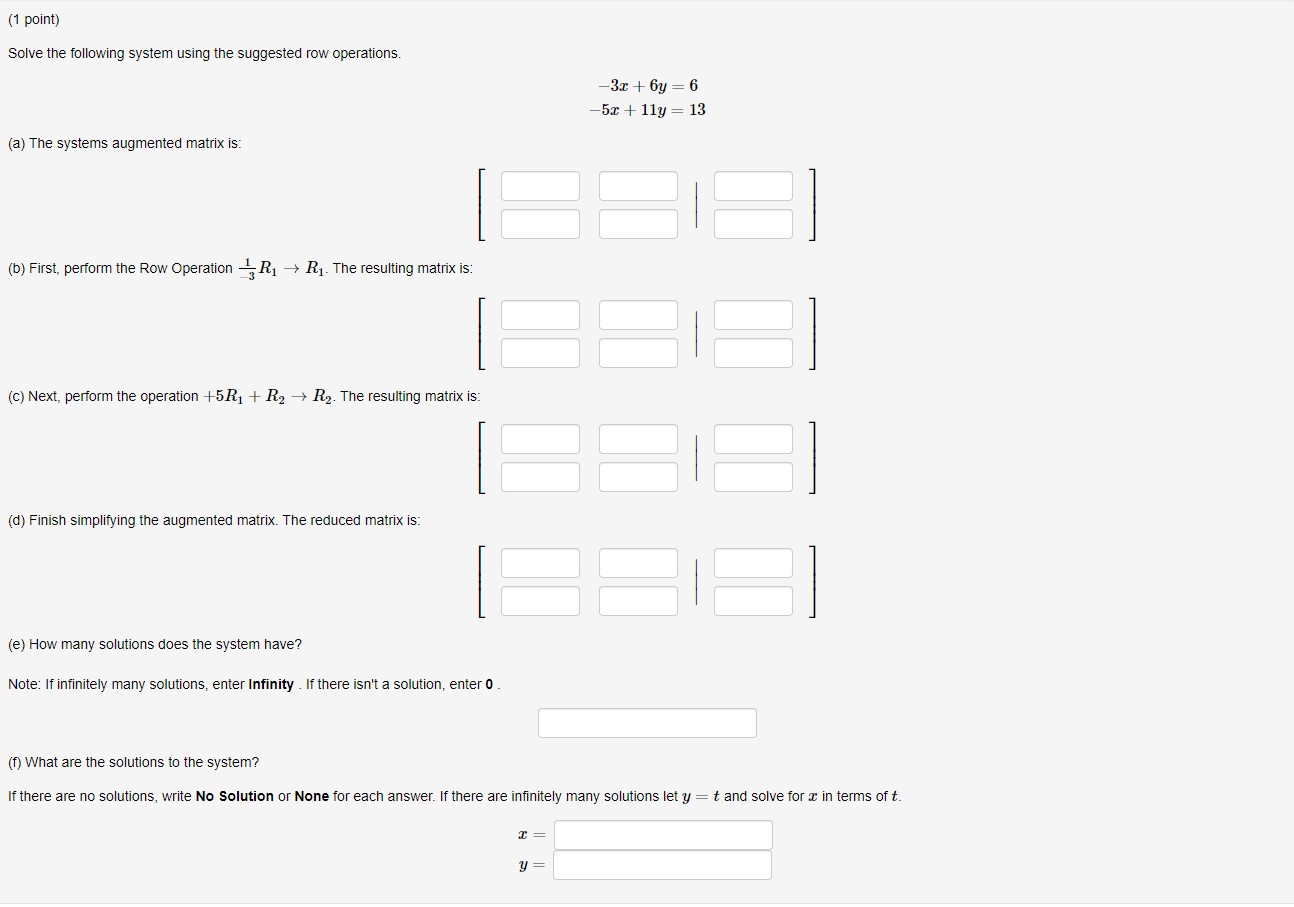
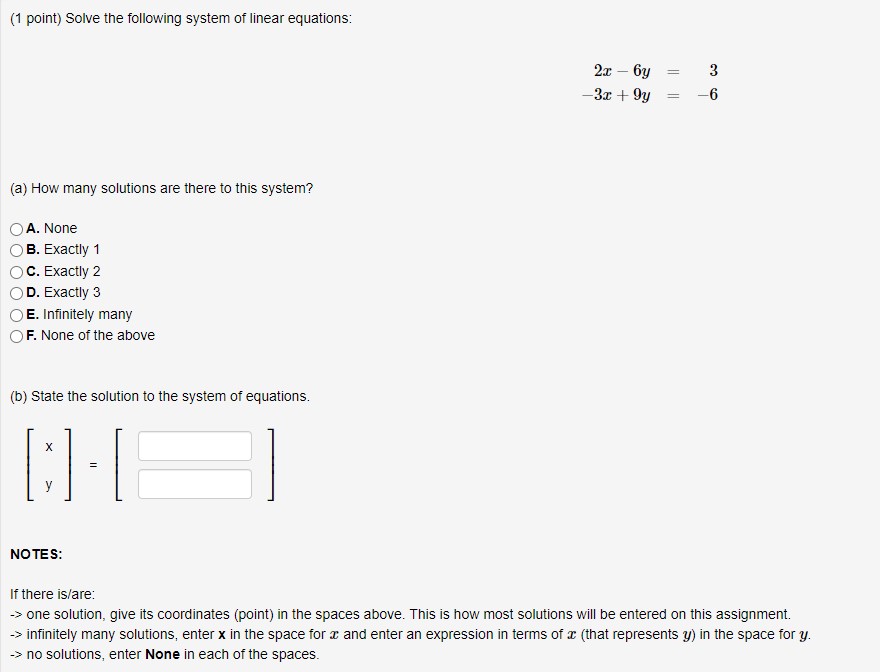
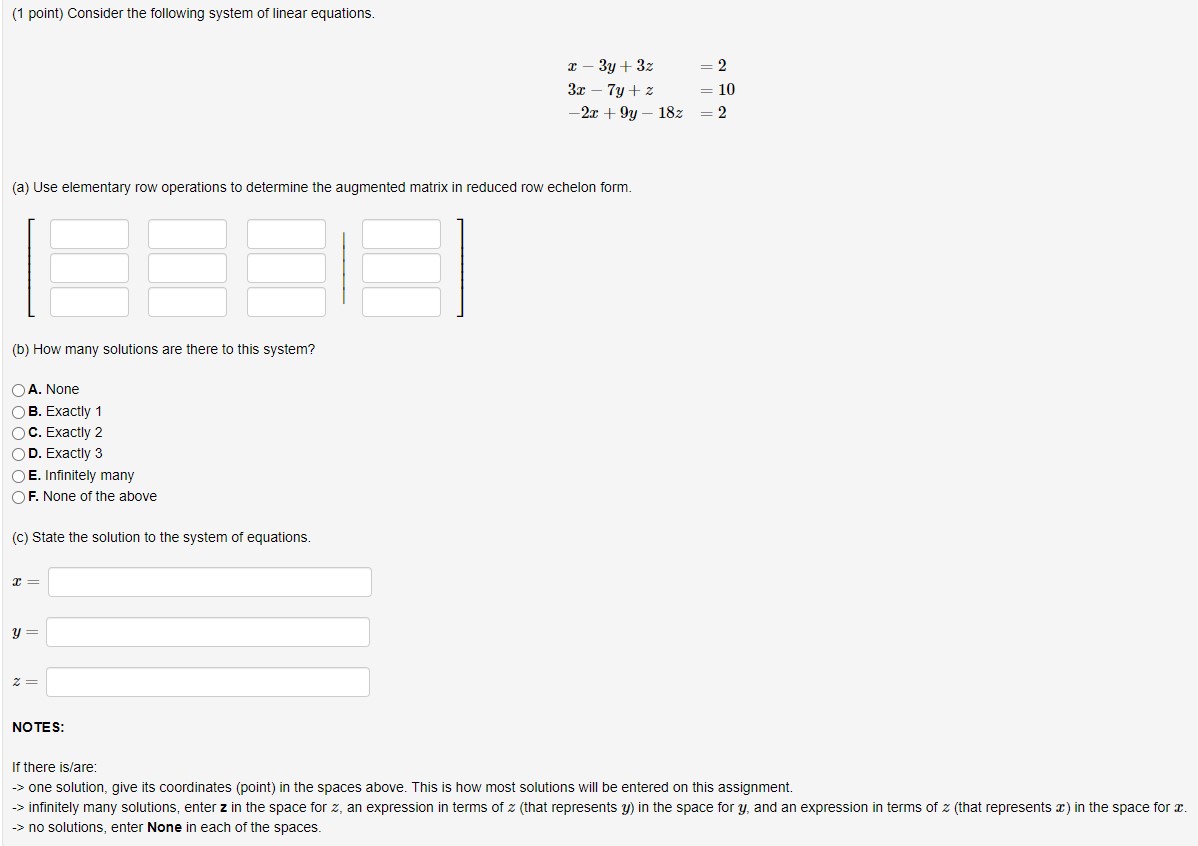
(1 point) FOR EACH PROBLEM ON THIS ASSIGNMENT, ENSURE THAT YOU TAKE NOTE OF HOW MANY ATTEMPTS ARE GIVEN. SOME OF THE PROBLEMS MAY ONLY ALLOW FOR ONE OR TWO ATTEMPTS DUE TO THE NATURE OF THE PROBLEM. Consider the following system of linear equations: 45y +21z = -84 76y -6z = 3 -45x +552 = 7 State the augmented matrix representing the system.(1 point) Express the following vector equation as a system of linear equations. T1 (Keep the equations in order.) D, = =(1 point) Solve the following system using the suggested row operations. -3x + 6y = 6 -5x + 1ly = 13 (a) The systems augmented matrix is: (b) First, perform the Row Operation - R1 - R1. The resulting matrix is: (c) Next, perform the operation +5R, + R2 - R2. The resulting matrix is: (d) Finish simplifying the augmented matrix. The reduced matrix is: (e) How many solutions does the system have? Note: If infinitely many solutions, enter Infinity . If there isn't a solution, enter 0 (f) What are the solutions to the system? If there are no solutions, write No Solution or None for each answer. If there are infinitely many solutions let y = t and solve for a in terms of t. y =(1 point) Solve the following system of linear equations using Gaussian elimination or Gauss-Jordan elimination. 6x + 4y = 14 9x + 6y = 21 X NOTES: If there is/are: -> one solution, give its coordinates (point) in the spaces above. This is how most solutions will be entered on this assignment. -> infinitely many solutions, enter x in the space for c and enter an expression in terms of a (that represents y) in the space for y. -> no solutions, enter None in each of the spaces.{1 point) Solve the following system of linear equations: Jew HH +l 53 ll ll | mm {a} HOW many solutions are there to this system? Q A. No ma 0 El. Exactly 1 Q o. Exactly 2 O o. Exactly 3 Q E. Innitely many 0 F. None of the above {t1} State the solution to the system of equations. NOTES: If there isl'are: } one solution, give its coordinates {point} in the spaces above. This is how most solutions will be entered on this assignment. :> innitely many solutions, enter: in the space for z and enter an expression in terms of a (that represents 3;} in the space for y. > no solutions, enter None in each of the spaces. (1 point) For each of the following systems of equations, determine whether it has no solution, an infinite number of solutions, or a unique solution. -10 + 10 y = 4 Select Answer v 1. 20 r - 20 y -10 Select Answer Infinite Solutions No Solution -5 c + y = 2 2. Unique Solution + 7y = -3 10r + 10y = Select Answer v 3. 20 c 20 y = -8(1 point) Determine the value of / such that the augmented matrix below represents a system of linear equations with infinitely many solutions. 8 (5 09 h 12 h =(1 point) Fred and Tonya are brother and sister. Fred has three times as many sisters as brothers, and Tonya has as many brothers as sisters. How many boys and girls are there in this family? Answer: boys and girls.(1 point) The augmented matrices of four systems of linear equations are given below. For each system, how many solutions does it have? 0 19 o 0 1 15 O 0 0 0 OA. Unique solution OB. Infinitely many solutions O C. No solutions OD. None of the above 1 0 13 0 1 -2 OA. No solutions O B. Unique solution O C. Infinitely many solutions O D. None of the above 18 OA. Unique solution OB. No solutions O C. Infinitely many solutions OD. None of the above 0 10 0 0 17 A. No solutions OB. Unique solution O C. Infinitely many solutions D. None of the above(1 point) Consider the following system ol linear equations. z3y+3z =2 3::79+z =10 2:I:+9y18z =2 (a) Use elementary row operations to determine the augmented matrix in reduced row echelon form. (b) How many solutions are there to this system? Q A. None 0 B. Exactly 1 O c. Exactly 2 O o. Exactly 3 O E. Innitely many 0 F. None of the above (1:) State the solution to the system of equations. 2: NOTES: If there islare: _> one solution, give its coordinates (point) in the spaces above. This is how most solutions will be entered on this assignment. > innitely many solutions, enter: in the space for z, an expression in terms of z (that represents y) in the space for y, and an expression in terms of z (that represents 3) in the space form. > no solutions, enter None in each of the spaces. (1 point) Solve the following system of linear equations using Gaussian elimination or Gauss-Jordan elimination. x - 2y 3 3y + z = I - 2z = 3 X NOTES: If there is/are: -> one solution, give its coordinates (point) in the spaces above. This is how most solutions will be entered on this assignment. -> infinitely many solutions, enter z in the space for z, an expression in terms of z (that represents y) in the space for y, and an expression in terms of z (that represents a) in the space for c. -> no solutions, enter None in each of the spaces.{1 point} Considers linear system whose augmented matrix is For what value of is will the system have no solutions? In: (1 point) Consider the homogeneous system of equations with coefficient matrix: 1 1 -5 1 A = 2 2 -10 2 [Recall: A homogeneous system is one where the right hand side of each equation is 0.] Find the solution to the corresponding homogeneous system of equations by expressing A in RREF. =T +s where r, s, te R. C3(1 point) Consider the homogeneous system of equations with coefficient matrix -4 6 -3 A = -3 -12 18 -12 [Recall: A homogeneous system is one where the right hand side of each equation is 0.] (a) State the number of variables in the homogeneous system of equations. Number of Variables n = (b) Determine the rank of A. Rank = (c) Use the results in parts (a) and (b) to determine the number of parameters in the general solution to the system of equations. Number of Parameters k =(1 point) For each of the following systems of equations, determine whether it has no solution, an infinite number of solutions, or a unique solution. 10x + 10y = Select Answer 1. 20 c 20 y = -10 -5x + y = Select Answer v 2. + 7y = Select Answer Infinite Solutions No Solution 10x + 10y = 4 3. Unique Solution 20 x - 20 y = 8